There’s a lot of math here but I have been able to recreate the Steig 3PC satellite reconstruction to a fair degree of accuracy. The satellite data consists of 5509 columns of 300 values which according to Jeff C RegEM chokes on. Fortunately, we don’t have to use all 5509 columns. The satellite reconstruction as presented by Steig09 can be recreated from the three principal components as shown at this link. Since Steig refuses to provide code for processing to the point of denying that it even exists, much of the process was developed by several different people through guessing and testing. I have included the some of the presently recreated yet non-existent code in this post.
Satellite Temperature Trend Also Halved by Simple Regridding
This is done by calculating the principal components of the satellite data and using RegEM to allocate station trends according to the high frequency covariance (a subject which needs more time). Anyway thanks to SteveM and about a dozen papers and articles I’ve learned a great deal about principal components. The first step then is to do a PC analysis of the well processed raw AVHRR satellite data. Below is a graph of the 3 PCs from the raw data and those of the Reconstruction data presented by Steig09.

Visually they are very similar. This is the code used in the analysis starting with the download and anomaly calc.
#download.file(“http://faculty.washington.edu/steig/nature09data/data/cloudmaskedAVHRR.txt”,”cloudmaskedAVHRR.txt”)
satraw = read.table(“cloudmaskedAVHRR.txt”)
satraw = ts(satraw, start=1982,freq=12)calc.anom =function(tsdat) {
anom = tsdat
for (i in 1:12) { sequ = seq(i,nrow(tsdat),12)
anom[sequ,] = scale(tsdat[sequ,],scale=F) }
anom}satraw_anom = calc.anom(satraw)
Then calculate the principal components. I’ve removed some of the checks in the code for clarity.
####################################################
####################################################
###satellite data pca
####################################################
####################################################
m=t(satraw_anom)
svd0=svd(m)PCAcurves=t((svd0$d) * t(svd0$v))
### pcacurves is the PCs with the righ singular vectors V multiplied through
PCActs=ts(PCAcurves,start=1982,deltat=1/12)##make singular vectors a time series
plot(PCActs[,1:10])#demonstrates that columns are the singular vectors
dim(PCActs) #300,300##svd0$u columns become loading values at each point
##check to see if multiplying UDV works – first 10 PC’s only
testpca= ts(t(t(PCActs[,1:10])*(svd0$u[1,1:10])),start=1982,deltat=1/12)
tt=ts(rowSums(testpca),start=1982,deltat=1/12)
plot(tt,type=”l”)
lines(satraw_anom[,1],col=”red”)#check pca rebuild
#everything checks
I performed a simple visual check at the end. This places PC’s into PCActs in an array. The next step was to place these satellite PC’s next to the 42 surface stations for RegEM.
tsu=ts.union(anomalies$surface,PCActs[,1:3])
dim(tsu)#600,20
#write.csv(tsu,”C:/agw/antarctic paper/Sat data code/PC recon/42 surface three sat pcs.csv”)
The RegEM process recreates all the pre 1982 data shown in Figure 1 above. As a verification of what visually looks like a reasonable match to the PC’s, I made the following plots.
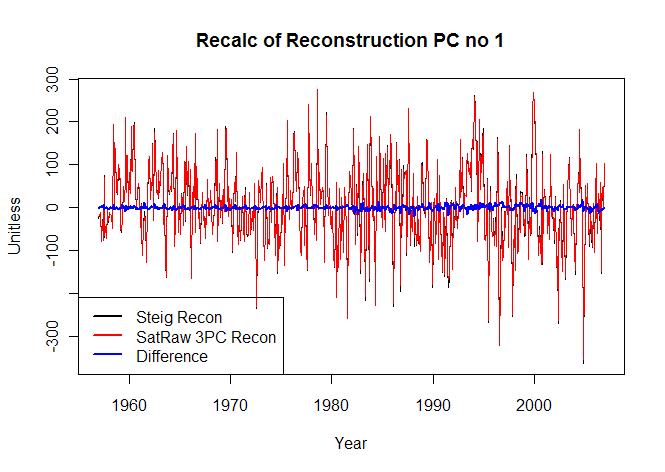
The 3 PC’s are close but not exact matches. With no better match and no clue idea about what causes the problem, the next step is to perform the reconstruction of the satellite temperature from the RegEM reconstruction. Here’s the code for the above graphs leading into the reconstruction.
Calc and Plot 3PC’s
recpc=read.csv(“C:/agw/antarctic paper/Sat data code/PC recon/regem regpar=3 sur full sat 3pc.csv”,header=FALSE)
rects=ts(recpc,start=1957,deltat=1/12)
dim(rects)#600,45 the first 42 cols are surface station the second 3 are regem sat
##################################
threesatpcts=rects[,43:45]
plot(threesatpcts)
##################################
##################################
#compare to steig reconstruction
svd2=svd(sat_recon)
plot(svd2$d)
plot(svd2$u[,3],type=”l”)
eigs=t(t(svd2$u)*(svd2$d))
plot(eigs[,3],type=”l”)
eigs=ts(eigs[,1:3],start=1957,deltat=1/12)plot(threesatpcts[,1],main=”Recalc of Reconstruction PC no 1″,xlab=”Year”,ylab=”Unitless”)
lines(eigs[,1],col=”red”,lwd=1)
lines(threesatpcts[,1]-eigs[,1],col=”blue”,lwd=2)
legend(“bottomleft”,lwd=2,c(“Steig Recon”,”SatRaw 3PC Recon”,”Difference”),col=c(“black”,”red”,”blue”))
#savePlot(“C:/agw/antarctic paper/pics/reconstruction/PC1 difference.jpg”,type=”jpg”)plot(threesatpcts[,2],main=”Recalc of Reconstruction PC no 2″,xlab=”Year”,ylab=”Unitless”)
lines(-eigs[,2],col=”red”,lwd=1)
lines(threesatpcts[,2]+eigs[,2],col=”blue”,lwd=2)
legend(“bottomleft”,lwd=2,c(“Steig Recon”,”SatRaw 3PC Recon”,”Difference”),col=c(“black”,”red”,”blue”))
#savePlot(“C:/agw/antarctic paper/pics/reconstruction/PC2 difference.jpg”,type=”jpg”)plot(threesatpcts[,3],main=”Recalc of Reconstruction PC no 3″,xlab=”Year”,ylab=”Unitless”)
lines(eigs[,3],col=”red”,lwd=1)
lines(threesatpcts[,3]-eigs[,3],col=”blue”,lwd=2)
legend(“bottomleft”,lwd=2,c(“Steig Recon”,”SatRaw 3PC Recon”,”Difference”),col=c(“black”,”red”,”blue”))
#savePlot(“C:/agw/antarctic paper/pics/reconstruction/PC3 difference.jpg”,type=”jpg”)
Then reconstruct the 5509 series from the weightings derived in the original singular value decomposition.
#######################################
#######################################
#reconstruct full antarctic from 3 svd pcs and RegEM
satreconId=array(0,dim=c(600,5509))for (i in 1:5509)
{
pcarec= ts(t(t(threesatpcts)*(svd0$u[i,1:3])),start=1956,deltat=1/12)
satreconId[,i]=ts(rowSums(pcarec),start=1956,deltat=1/12)
}
Calculate the full antarctic trend from the reconstructed data.
#########################################
#########################################
#check full trend
jj=rowMeans(satreconId)
jj=ts(jj,start=1957,deltat=1/12)
coef(lsfit(time(jj),jj))[2] #.0107#plot trend
plot(jj,main=”Temperature Anomaly of Antarctic\nReconstruction From Raw AVHRR”,xlab=”Year”,ylab=”Anomaly C”)
abline(lsfit(time(jj),jj),col=”red”,lwd=2)
text(1965,-3,paste(“Trend C/Dec =”,round(coef(lsfit(time(jj),jj))[2]*10,3)),col=”red”)
#savePlot(“C:/agw/antarctic paper/pics/reconstruction/Raw Recon Trend.jpg”,type=”jpg”)
The reconstructed antarctic trend created by the above plot looks like this.

Steig 09 reports a trend:
The continent-wide trend is 0.12 +/- 0.07 uC per decade.
From the reconstructed data I calculated a trend as well. The code is below.
First load the data directly from Steig’s site.
download.file(“http://faculty.washington.edu/steig/nature09data/data/ant_recon.txt”,”ant_recon.txt”,mode=”wb”)
#scan in satellite data
grid=scan(“ant_recon.txt”,n= -1) # 37800
dim(grid)=c(5509,600)
grid=t(grid)
fgrid=grid#600*5509 #[1] 3305400
sat_recon=ts(array(grid,dim=c(600,5509)),start=c(1957,1),freq=12)
Calculate the annual mean temps and average them into vector ‘kk’. Perform least squares and plot.
#Steig recon trend
kk=rowMeans(sat_recon)
kk=ts(kk,start=1957,deltat=1/12)
coef(lsfit(time(kk),kk))[2] #.0107#plot trend
plot(kk,main=”Temperature Anomaly of Antarctic\nSteig’s Reconstruction as Presented”,xlab=”Year”,ylab=”Anomaly C”)
abline(lsfit(time(kk),kk),col=”red”,lwd=2)
text(1965,-3,paste(“Trend C/Dec =”,round(coef(lsfit(time(kk),kk))[2]*10,3)),col=”red”)
#savePlot(“C:/agw/antarctic paper/pics/reconstruction/Steig Recon Trend.jpg”,type=”jpg”)plot(kk-jj,main=”Difference in Temperature Anomaly of Antarctic\nSteig’s – Id”,xlab=”Year”,ylab=”Anomaly C”,ylim=c(-4,4))
abline(lsfit(time(kk),kk-jj),col=”red”,lwd=2)
text(1965,-3,paste(“Trend C/Dec =”,round(coef(lsfit(time(kk),kk-jj))[2]*10,3)),col=”red”)
#savePlot(“C:/agw/antarctic paper/pics/reconstruction/Recon Difference Trend.jpg”,type=”jpg”)
This is the first graph from the above code.

The slope of 0.118 confirms the 0.12 reported in Steig 09. The second plot from the above code is the difference between the reconstructions.

As you can see, the reproduction of Steig’s reconstruction is close but not perfect.
The spatial distribution of temperature trend from Steig09 is calculated by least squares fit to the trend of each of the 5509 series as shown below.
tr=array(0,dim=5509)
satreconId=ts(satreconId,start=1957,deltat=1/12)
for(i in 1:5509)
{
tr[i]=coef(lsfit(time(satreconId),satreconId[,i]))[2]*10
}tempx.plot(dat=tr*26/.4,xy=sat_coord,titl=”RegEM Surface Station Recon 3PC’s Trend/Decade”,low=-.4,high=.4 )
#savePlot(“C:/agw/antarctic paper/pics/reconstruction/Antarctic Spatial Trend from Raw.jpg”,type=”jpg”)
The code is repeated for the Steig reconstruction.
###########################################
###########################################
#plot antarctic steig recon trend
trs=array(0,dim=5509)
for(i in 1:5509)
{
trs[i]=coef(lsfit(time(sat_recon),sat_recon[,i]))[2]*10
}tempx.plot(dat=trs*26/.4,xy=sat_coord,titl=”RegEM Surface Station Recon 3PC’s”,low=-.4,high=.4 )
#savePlot(“C:/agw/antarctic paper/pics/reconstruction/Antarctic Spatial Trend from Steig.jpg”,type=”jpg”)
And the result of this code are the following two plots. The first is from the reconstruction from the raw data.

Figure 9 is from the Steig reconstruction as presented.
I didn’t get as much warming south of the mountain range but it’s pretty clear I’m close. Thanks to Steve McIntyre, RomanM, Jeff C, Ryan O and anyone else I forgot for your help in developing the math this far. These are actually the same calculations I used in my previous post, What’s Wrong with RegEM, however I skipped ahead of the replication. Once I had verified the 3 PC’s shortly after the data was released, I lost a bit of interest in repeating the reconstruction all the way through and skipped ahead. Thanks also to those who requested that I go back and dot my i’s.




Jeff,
I can’t say that I follow the math, I’m a novice in R, but job well done!!
Jeff, how much of the difference could be due to the specific station data that they used? As well, I appreciate that they might have dine some infilling on the stations before feeding it to RegEM.
#2, I’m not sure. The Steig AVHRR reconstruction data which you originally calculated the 3 pc’s from results in slightly different PC’s than I calculated. Since I can’t figure out how they would have included surface station data in that 3 PC derivation, I think the satellite data may not be exactly the same.
I’ve been considering possibly doing something crazy like deriving the PC’s with the complete surface stations in the matrix but it just doesn’t make sense.
Perhaps I should try the huge matrix version for RegEM, Jeff C said it didn’t work and I got stuck replacing NA from R with NaN for matlab. I’ve been doing it in Excel. For some reason after the replacement R couldn’t make a good file for Matlab.
Wouldn’t it be nice just to see the code?
I don’t understand. You can output data from R using write.table into a text file and replace NAs with NaNs in the process.
How exactly are you using the station data? I tried simply combining the uninfilled satation data with the fhree PCs into a single matrix which I ran through my (not properly written) version of R Regem and it ran and converged reasonably. I also tried running the station data by itself to infill and then ran it with the 3 PCs. Today I think I found and fixed the problem with my ttls script and I will try it again tomorrow afternoon.
I combined unfilled station data 42 series with 3 pc’s of sat data, replaced NA’s with NaN’s in excel and ran Matlab.
The NA NaN thing was just a minor software headache but I spent an hour or so one day trying. R was putting in quotes, it’s a minor thing just an irritation. Jeff C apparently was able to do it and Matlab just crashes.
I did a crazy reconstruction by RegEM’ing the station data broken down into 20pcs and the sat data into 20. I was able to do high order RegEM and get it to converge but the results were what really started to convince me of the Low/High freq trend problem with RegEM. It really put a stop to the fun.
Eyeballing the spatial reconstructions, Steig’s gives a little more warming to the peninsula and west antarctic, and slightly less warming in the east when comparing to Id Recon. What would you have to do with raw data to recreate this tilting of trend?
#7 I like this question.
Since from my previous post I learned that long term trends are basically randomized, I’d say…anything.
I really have no idea of a direct influence that would do it, there are too many possibilities. Any one station could correlate less… or more …or a group of stations… or the slight variation in the sat data… or perhaps my method is slightly different.
It’s pretty humorous really.
Splendid work. Do you have one of the PC2s flipped upside down in figure 1?
The trend difference from #7 is somewhere in the differences of the PC2’s and PC3’s. The PC 3 difference plot stands out the most I think. Despite the small amplitude of pre 1982 in both PC 3’s, the pre-1982 differences are fairly large by comparison. Have you re-visited the un-natural pre 1982 PC3 issue recently?
Could you try running the reconstructions omitting the pre-1982 PC3 (or setting to 0) for both Id and Steig to see if this tightens up the trends and the spatial tilting?
Great work Jeff. More comment to come a bit later, but for now, here is how you solve the NA/NaN problem.
write.csv(anom14_5509,”anom14_5509_matlab.csv”,na=”NaN”,row.names=F,col.names=F)
I think I know why the Schneider RegEM fails on the big data set – but this is just one more piece of evidence that they didn’t feed the “raw” AVHRR into the RegEM grinder. I’ll write this up tomorrow.
This is very good stuff.
BTW don’t assume that you will ever be able to reconcile results in an engineering sense. No one’s been able to do so with MBH, tho both we and Wahl/Ammann get results that are close (Wahl and Ammann results reconcile to 8 nines to ours, so reconciling is possible.)
In the Mann case, Nature required them to produce the data and, after Mann’s WSJ refusal to disclose his “algorithm”, the House Energy and Commerce Committee required him to produce his code. But the code didn’t work with the data as archived and there remain loose ends. My guess (one shared by Jean S and UC who followed this) is that the data eventually archived is somewhat different from the data version used in the original article and that no one has a copy anymore of the data as originally used.
I mention this episode because there’s a possibility that the AVHRR version archived in late March is different in some respects from the version used to do the article. If that’s the case, it will never be possible to precisely reconcile. The only way to be sure is to see the realcode, but I doubt that we’re going to.
#11. Another way of solving the NA problem is what the Fortran programmers do. Set the NA values to a grotesque negative number -99999 and then handle the -99999 as usual.
Stephen McIntyre said
April 6, 2009 at 4:12 am
#11. Another way of solving the NA problem is what the Fortran programmers do. Set the NA values to a grotesque negative number -99999 and then handle the -99999 as usual.
NOOOOO we would never do that!!!!! lol….. 99999 and out!!!!!
Ok now that you’ve recreated what he’s done, what can you tell us about how BS his work is and exactly how and where he’s doing it?
Jeff, I’m not following all the details but are you able to repeat this fig 8 with increasing numbers of PCs, eg 5,7,9,11 ? That would be really interesting.
#16, I don’t want to say anyones work is BS at this point. I do believe the math may have a serious problem which if it proves out would lead to incorrect trends.
See the What’s wrong with RegEM post.
PaulM, I did the analysis with 10 in ‘What’s wrong with RegEM’ link above and ran into some interesting trouble which has somewhat stopped me in my tracks with RegEM.
#17, Is the link your name goes to your work. What’s it from?
Great job, Jeff! Whether or not Steig09’s ant_recon.txt is meaningful or robust, at least you have shown that it can be replicated (closely enough for practical purposes) from cloudmaskedAVHRR.txt + 42 surface stations.
I’m surprised that your PC3 comes out just as flat as Steig’s — yours is even flatter, in fact. This is very strange, since there is no comparable reduction in variance in the other 2 PC’s. Do you have any idea why this occurs? I had assumed that it had been manually zeroed out somewhere along the way, but apparently this is not the case.
Your blue&red graphs comparing your 3PCs to Steig’s make it look like the fit is much worse for PC2 and PC3 than it is for PC1. However, these PCs act on very different singular values in their contribution to temperature. If each PC were multiplied by its singular value, the PC2 and PC3 graphs would be scaled down to where the “Difference” lines in the 3 graphs looked much more alike.
One variant I hope you have time to do now is to try omitting the 5 non-Antarctic oceanic stations Steig included in his 42, to see how much difference they made. Amsterdam at 52N would not be included in a study of Arctic temperatures, so why did Steig & Co. include Campbell Island at 52S in this study?
PS: What time zone is your server in? Greenland Daylight Time??
(posted at 11:14 AM EST)
Another interesting variant, to illustrate the oversmoothing effect of too few PCs, would be to run it with just 1 PC, and then plot both the trend map and the continent-wide average with its trend line.
Given that your 20/10 run in your April 4 post “What’s Wrong with RegEM” gives a much lower trend than this 3/3 run, RegEM appears to be not just smearing the Peninsula over the whole of the continent, but to be somehow multiplying its effect in the process. So I would predict that 1/1 would make the whole continent look even more like the Peninsula, and to jack up the trend even higher than Steig’s +0.12dC/decade.
PS: I guess now that your server is on Greenwich Mean Time, which doesn’t do DST?
Hu, I tried to reset the time, we’ll see after this post. I’m in US central, the server is in orbit on a Kolondan mothership – don’t tell anyone.
As far as RegEM, you might be the best person to talk with. Surface stations are weighted according to covariance with the sat data. There is a strong concentration of surface stations in the peninsula.
Assume for now that covariance is entirely separate from long term trends. There is some evidence for this in that temps oscillate back and forth across the mountain range in the 3 PC version of the data. So we get negative correlation from stations on either side of the mountains and potentially both sides of the mountains are warming long term. But just for the purpose of this comment assume it’s true.
RegEM only cares about the dominant covariance so if both sides of the antarctic mountains had equal positive trends a negative trend would be copied from south to north and again from north to south. Canceling the local positive trends to some degree.
Now if we look at higher order RegEM we do localize the data better, more distant stations are decorrelated better but the problem occurs with the negative correlation and we get things like extreme cooling of the Ross ice shelf (see whats wrong with RegEM).
If we consider the problem with single PC reconstruction, it might makes the most sense but would end up basically averaging all the trends together without regard to location. If we did it with the full dataset you would still get odd negative correlations receiving improper weighting. If the pos/neg cycles were split 50/50 across a continent the weighting of ever higher PC’s where the continent had a continuous uptrend would net to zero.
I don’t know if that makes any sense.
—-
I have an idea for fixing the reconstruction now. Take the full sat data and correlate each surface station to it. Weight each surface station according to the correlation and average (handling the NA’s carefully). Negative correlations will be assumed to have zero effect on the local station.
This method would do precisely what Steig09 intended but with much simplified math and no throwing away important covariance data by PCA. Also the reconstruction would be entirely surface station data so satellite trends would be nearly moot.
Any thoughts?
Jeff – I’ve updated my flow diagram based upon what we have learned over the past few weeks and some presumptions. What you have done in this post is shown on the right-hand side of the heavy dashed line in the diagram.
If anyone has any changes or comments let me know. I’m attempting to document what we think we know before it is forgotten.
Jeff, there is no real difference in output between your replication and the original. Outstanding.
.
BTW, the Ross Ice Shelf cooling from your earlier post may actually be real. I got the same thing simply by properly calibrating the raw AVHRR data to the ground stations. Steig’s AWS recon, which doesn’t use satellite data, also shows cooling post-1982 on Ross, and a couple of the West Antarctic stations are negative as well.
Oh, and a BTW . . . the models predict a local minimum at the Ross Ice Shelf. Just think . . . you could be confirming models. Haha. 🙂
23: Maybe there is some major source that “starts” when the PC shows variance and does not exist before that? So that a PC would capture flat before that and variation after?
I mean a source of data, not a forcing.
I am certain that Steig simply used RegEM on a combination of the data from the 42 surface stations and the 3 PCs for 1982-2006 that he derived from processing the satellite data. That method, rather than using the full (cloudmasked) satellite data as an input to RegEM, is in line with what his paper implies as to his method (as per the Mann 2007 JGR article Steig refers to). Using RegEM on a combination of the surface station data (excluding Gough and Marion)sourced from that archived at Climate Audit (“sanom” as per Jeff C’s 16 February post) and the 1982 to 2006 section only of the 3 satellite data PCs derived from the last 300 months of Steig’s satellite reconstruction (using prcomp), I get reconstructions of the 3 satellite PCs for 1957 to 1981 that are almost identical (within linear combinations of each other) to those derived from Steig’s reconstruction. Only 0.4% of the total variance of Steig’s 3 reconstructed 1957-1981 satellite PCs is unexplained by my RegEM output, using 50 iterations. This should be simple to reproduce, but I can post R code once I have recreated and tidied it up, if that would be of interest.
I have also investigated the effect on the antarctic wide temperature trend that would have resulted from Steig’s satellite based reconstruction (using his 3 satellite PCs) if various changes had been made to the surface stations that are included in the RegEM input. Omitting the 5 island stations and also all the peninsular stations only reduces the average trend from 0.1174 to 0.087 degrees C per decade. I also tried adding a dummy series with a linear trend of 1 degree C/decade over the whole 50 years, using all 42 surface stations. Doing so substantially increased the average trend of the satellite based rconstruction, to 0.197 degrees C per decade, despite the dummy series being only one out of 43 (46 including the 3 PCs) and having no high frequency correlation with any other series. I find that rather alarming.
#30, That’s interesting.
I used 3 pc’s in my reconstruction as well. Are you getting a closer result? It sounds like the same method, perhaps I could have let RegEM converge farther b/c I don’t think it ran for that many iterations.
#28 The source is the boundary between the sat and surface stations. Sat data only exists post 82.
#28 and #32
Don’t forget that the spatial grid weighting changed the shape of the PC3 and that 95% of the surface stations (the only real data pre-1982) fall into areas of low vector weighting in virtually all of the 3 eigenvectors.
how can I forget what I never learned in the first place…
#30 Nic L.
Uhm… I was trying to block quote the following from Nic L:
“I also tried adding a dummy series with a linear trend of 1 degree C/decade over the whole 50 years, using all 42 surface stations. Doing so substantially increased the average trend of the satellite based rconstruction, to 0.197 degrees C per decade, despite the dummy series being only one out of 43 (46 including the 3 PCs) and having no high frequency correlation with any other series.”
#36,
I agree, I was waiting for a reply from Nic and wanted a better understanding of his results. If he’s got a better mousetrap or even the same one, I’m interested.
Re Nic L (#30), it looks like you have confirmed Jeff Id’s replication of Steig ant_recon.txt using 3 PC’s of cloudmaskedAVHRR.txt, Nic. Is 0.1174 the continent-wide trend you are getting? If so, you are even closer to Steig than Jeff. (I get 0.1178 using ant_recon.txt directly, though I see Ken Fritsch is getting 0.11818, which is puzzling.)
You write,
That turns out to be an important reduction, given that the AR(1) serial correlation-adjusted standard error for Steig’s trend is 0.0458. (See my “Steig 2009’s non-correction for serial correlation” on CA.) Twice this is 0.0916, which falls short of 0.1174 or 0.1178 or 0.1182, but clearly exceeds 0.087.
But Steig et al admit there is warming from the Peninsula, which at least is part of Antarctica. What happens when you just omit the 5 non-Antarctic oceanic stations that Steig included?
Steig’s table S2 names the 42 occupied stations used as predictor variables, plus 4 AWS that are included in the table for unstated reasons. (These are Mt. Simple, Siple, Byrd AWS, and Harry.) I have a suspicion that these 4 AWS were in fact included with the 42 occupied stations in the reconstruction, otherwise why are they singled out to be in this list? Does the remaining small discrepancy shrink further when they are included (using the old Harry data Steig would have used)?
Re Hu McCulloch (#38),
Yes, I get a continent-wide trend of 0.1174 degrees C per decade over 1957 – 2006.
I will work on answering your other queries and post again later today. I am also trying to produce a stand alone script.
Nic, Thats interesting. I wonder if I let RegEM converge for longer I might get the same result.
Further to my earlier posts (#30 and #39) I have now tidied up and re-checked my script and calculations, and looked into Hu McCulloch’s questions (#38). Most of my results stand, but it seems that originally I derived the satellite based PCs for 1982-2006, and the weights of the 5509 temperature series on those PCs, by PCA on Steig’s reconstruction over 1957-2006 rather than just over 1982-2006 (only the latter period being based exclusively on actual satellite data – ignoring the 3 months that I gather were missing in 1994). Doing so effectively incorporated results from Steig’s RegEM infilling into my RegEM based reconstruction. Upon correcting this misake, the continent-wide average decadal temperature trend changes from 0.1174 to 0.1257 degrees C, over 1957-2006. The statistical fit remains close, with all but 0.3% of the variance in monthly average temperatures over the infilled period 1957-1981 explained by my RegEM output, and the range of differences between my calculated average temperatures and those per Steig’s reconstruction being 0.446 degrees C. The derived 1957-1981 PCs in my reconstruction are also very similar to those per Steig’s reconstruction, allowing for my PCs to be linear combinations of his and vice versa rather than there being a pure correspondence between the PCs.
Removing just the 5 island stations leaves the 1957-2006 average decadal temperature trend little changed, at 0.1268 degrees C.
Omitting the 5 island stations and also all the peninsular stations reduces the 1957-2006 average decadal trend to 0.0889 degrees C, slightly higher than the 0.087 I reported earlier.
Adding a dummy series with a linear trend of 1 degree C/decade over the whole 50 years, in addition to using all 42 surface stations, substantially increased the 1957-2006 average decadal trend of the satellite based reconstruction to 0.1974 degrees C, as reported previously.
I have also investigated the effect of including the four AWS listed in Steig’s table S2. The AWS data that I used is that which I had previously worked out Steig had used, which is different from that archived by Steve McIntyre at Climate Audit, so is not precisely reproducable in the absence thereof (although using AWS data archived at Climate Audit would probably give very similar results). I found that including this AWS data increased the 1957-2006 average decadal trend to 0.1351 degrees C. The range of differences between my calculated average temperatures and those per Steig’s reconstruction rose from 0.446 to 0.902 degrees C, showing a worse fit.
An R script that carried out the above noted calculations is given below. To use it, you must have imported Steig’s 600*5509 reconstruction as ant_recon. The final section will not work in the absence of the aws_so06a data file, but I can provide that on request.
# Derive surface station temperature anomalies using Jeff C’s script: omit this if you already have sanom
surf=Data$surface
surf=window(surf,start=1957,end=c(2006,12))
surf <- surf[,-26] #deletes column 26 – Marion
surf <- surf[,-17] #deletes column 17 – Gough
a=as.numeric(surf)
dim(a)=c(600,42)
surfanomaly=array(NA,dim=c(600,42))
for(i in 1:42)
{
b=a[,i]
dim(b)=c(12,50)
an=rowMeans(b,na.rm=TRUE)
surfanomaly[,i]=a[,i]-an
}
sanom=ts(surfanomaly,start=1957,deltat=1/12)
dim(ant_recon)[2] # 5509
av_ant_recon=rowSums(ant_recon)/5509
lm(av_ant_recon*10~time(sanom[,1])) # calculate the decadal trend in average antarctic temperature per Steig’s satellite based reconstruction
# Coefficients: (Intercept) time(sanom[, 1])
# -234.3800 0.1178
pcsath=prcomp(ant_recon[301:600,]) # derives the 3 PCs from Steig’s satellite based reconstruction based on actual data only
s=lm(av_ant_recon[301:600] ~ pcsath$x[,1:3]); s$coefficients # calculates the weights of the average antarctic temperature 1982-2006 on the 3 satellite PCs derived from the same period
#(Intercept) pcsath$x[, 1:3]PC1 pcsath$x[, 1:3]PC2 pcsath$x[, 1:3]PC3
#-1.255975e-11 -1.262435e-02 1.737021e-03 -3.307048e-03
z=lm(t(ant_recon[1:300,]) ~ pcsath$rotation[,1:3])# derives the 3 PCs from Steig’s satellite based reconstruction for 1957-1981, using the same weights as for 1982-2006
earlyPCs=t(z$coefficients[2:4,])
pcsath_ss2=array(dim=c(600,45)); pcsath_ss2=ts(pcsath_ss2,start=1957,frequency=12)
pcsath_ss2[,4:45]=sanom; pcsath_ss2[1:300,1:3]=NA # sets up the RegEM input matrix using the 42 surface station anomaly data and with the 3 satellite based PCs set to NA for 1957-1981
pcsath_ss2[301:600,1]=pcsath$x[,1]; pcsath_ss2[301:600,2]=pcsath$x[,2]; pcsath_ss2[301:600,3]=pcsath$x[,3]
#inserts the 3 reconstruction derived PCs for 1982 to 2006 (based on actual, not infilled, data), rescaled so that the weight of each PC on the average antarctic temperature is on the same scale as the surface station data
rpcsath_ss2=regem_pttls(pcsath_ss2,maxiter=50) # performs RegEM
av_pred=rpcsath_ss2[[51]]$X[,1:3]%*%s$coefficients[2:4] # derives the average temperature from the 3 PCs
PCtrends=lm(av_pred*10~time(sanom[,1])) # calculates the decadal trend 1957-2006
PCtrends$coefficients[2] # 0.125719
range(av_pred[301:600]-av_ant_recon[301:600])
#[1] 0.1017785 0.1017785 Confirms 1982-2006 satellite based average temperatures unaltered after RegEM save for shift in centering
range(av_pred[1:300]-av_ant_recon[1:300])
#[1] -0.1998979 0.2462105 Shows range of differences in my reconstructed 1957-1981 satellite based average temperatures is fairly small
anova.lm(lm(av_ant_recon[1:300] ~ av_pred[1:300]))
# Df Sum Sq Mean Sq F value Pr(F)
#av_pred[1:300] 1 333.11 333.11 94525 < 2.2e-16 ***
#Residuals 298 1.05 0.003524
fit=(lm(rpcsath_ss2[[51]]$X[1:300,1]*s$coefficients[2] ~ earlyPCs[,1]+earlyPCs[,2]+earlyPCs[,3])) # tests fit of my reconstructed 1957-1981 satellite PC1 to that from Steig’s reconstruction
fit$coefficients
# (Intercept) earlyPCs[, 1] earlyPCs[, 2] earlyPCs[, 3]
# 0.0727029431 -0.0126631895 0.0002223910 -0.0006261348
anova.lm(fit)
# Df Sum Sq Mean Sq F value Pr(F)
#earlyPCs[, 1] 1 334.42 334.42 1.6954e+05 < 2.2e-16 ***
#earlyPCs[, 2] 1 0.05 0.05 2.4474e+01 1.265e-06 ***
#earlyPCs[, 3] 1 0.02 0.02 7.7777e+00 0.005632 **
#Residuals 296 0.58 0.001972
fit=(lm(rpcsath_ss2[[51]]$X[1:300,2]*s$coefficients[3] ~ earlyPCs[,1]+earlyPCs[,2]+earlyPCs[,3])) # tests fit of my reconstructed 1957-1981 satellite PC2 to that from Steig’s reconstruction
fit$coefficients
# (Intercept) earlyPCs[, 1] earlyPCs[, 2] earlyPCs[, 3]
# 7.152243e-03 7.796776e-06 1.642119e-03 6.103736e-05
anova.lm(fit)
# Df Sum Sq Mean Sq F value Pr(F)
#earlyPCs[, 1] 1 0.00704 0.00704 143.8411 < 2e-16 ***
#earlyPCs[, 2] 1 1.14527 1.14527 23393.2761 < 2e-16 ***
#earlyPCs[, 3] 1 0.00015 0.00015 2.9778 0.08546 .
#Residuals 296 0.01449 0.00005
fit=(lm(rpcsath_ss2[[51]]$X[1:300,3]*s$coefficients[4] ~ earlyPCs[,1]+earlyPCs[,2]+earlyPCs[,3])) # tests fit of my reconstructed 1957-1981 satellite PC3 to that from Steig’s reconstruction
fit$coefficients
# (Intercept) earlyPCs[, 1] earlyPCs[, 2] earlyPCs[, 3]
# 1.721651e-02 -4.627822e-05 4.786071e-04 -3.784018e-03
anova.lm(fit)
# Df Sum Sq Mean Sq F value Pr(F)
#earlyPCs[, 1] 1 0.00414 0.00414 157.64 < 2.2e-16 ***
#earlyPCs[, 2] 1 0.57767 0.57767 22013.13 < 2.2e-16 ***
#earlyPCs[, 3] 1 0.56031 0.56031 21351.50 < 2.2e-16 ***
#Residuals 296 0.00777 0.00003
#Examine the effect of excluding the 5 island stations, nos 9,18,23,34,39
pcsath_ss2xi=pcsath_ss2[,c(1:11,13:20,22:25,27:36,38:41,43:45)]
rpcsath_ss2xi=regem_pttls(pcsath_ss2xi,maxiter=50) # performs RegEM
av_pred=rpcsath_ss2xi[[51]]$X[,1:3]%*%s$coefficients[2:4] # derives the average temperature from the 3 PCs
PCtrends=lm(av_pred*10~time(sanom[,1])) # calculates the decadal trend 1957-2006
PCtrends$coefficients[2] # 0.1270667
#Examine the effect of excluding the 5 island stations, nos 9,18,23,34,39, and the 15 peninsular stations, nos 1,3,7,12,14,15,16,17,20,21,24,26,33,35,37
pcsath_ss2xip=pcsath_ss2[,c(1:3,5:6,8:9,11,13:14,16,22,25,28,30:35,39,41,43:45)]
rpcsath_ss2xip=regem_pttls(pcsath_ss2xip,maxiter=50) # performs RegEM
av_pred=rpcsath_ss2xip[[51]]$X[,1:3]%*%s$coefficients[2:4] # derives the average temperature from the 3 PCs
PCtrends=lm(av_pred*10~time(sanom[,1])) # calculates the decadal trend 1957-2006
PCtrends$coefficients[2] # 0.08922327
#Examine the effect of adding a proxy that is a linear trend of 1 degree C per decade
pcsath_ss2t=array(dim=c(600,46)); pcsath_ss2t=ts(pcsath_ss2t,start=1957,frequency=12)
pcsath_ss2t[,1:45]=pcsath_ss2
pcsath_ss2t[,46]=seq(length=600,from=0, by=.00833333)
rpcsath_ss2t=regem_pttls(pcsath_ss2t,maxiter=50) # performs RegEM
av_pred=rpcsath_ss2t[[51]]$X[,1:3]%*%s$coefficients[2:4] # derives the average temperature from the 3 PCs
PCtrends=lm(av_pred*10~time(sanom[,1])) # calculates the decadal trend 1957-2006
PCtrends$coefficients[2] # 0.1988425
#Examine the effect of adding the 4 AWS listed in Steig’s table S2: Mt Siple, Siple, Byrd, Harry, using the data that I deduce Steig used (not as archived by Steve McIntyre)
pcsath_ss2aws4=array(dim=c(600,49)); pcsath_ss2aws4=ts(pcsath_ss2aws4,start=1957,frequency=12)
pcsath_ss2aws4[,1:45]=pcsath_ss2
pcsath_ss2aws4[277:600,46]=aws_so06a[,43]
pcsath_ss2aws4[277:600,47]=aws_so06a[,57]
pcsath_ss2aws4[277:600,48]=aws_so06a[,3]
pcsath_ss2aws4[277:600,49]=aws_so06a[,26]
pcsath_ss2aws4[1:276,46:49]=NA
rpcsath_ss2t=regem_pttls(pcsath_ss2aws4,maxiter=50) # performs RegEM
av_pred=rpcsath_ss2t[[51]]$X[,1:3]%*%s$coefficients[2:4] # derives the average temperature from the 3 PCs
PCtrends=lm(av_pred*10~time(sanom[,1])) # calculates the decadal trend 1957-2006
PCtrends$coefficients[2] # 0.1351401
range(av_pred[1:300]-av_ant_recon[1:300]) #[1] -0.5128852 0.3889841
#19, Jeff, sorry for not keeping up. That figure on the ‘whats wrong’ thread with the big blue (rather than red) area in W antarctica is really good.
#20 Yes I am collating that stuff, some of it is my ideas but most comes from elsewhere as mentioned at the end. There is an email at the end if anyone has comments and additional examples.