Nic L has done what I think you’ll find to be a very interesting analysis of GHCN data. All of these analyses should be considered preliminary because of the huge amount of data and unusual QC issues in the data. I’ve checked his code briefly and his version of the getstation should work fine with the mod parameter set. My older version had a problem in it that resulted in it ignoring the WMO version number. There are a couple of other QC issues with the data that this getstation function doesn’t attempt to repair, but they should not affect the results.
In the meantime, It’s very interesting what Nic found. Consider that old GISS had 1934 vs 1998 ratios of 1.4 : 0.9 – Nic’s results mirror their original. Gissmatic.
—————-
Long Record GHCN Stations – an Analysis of the Data
At Jeff’s request, I present here some findings from work I have carried out using long-record GHCN stations. I have defined these as stations with temperature data in both 1900 and 1999 and fewer than 240 months (20%) in that period with no data. The reason for looking at long record stations is primarily that one can have some confidence that trends over the last 100 years or so reflect actual changes in recorded temperature and are not affected by changes over time in the set of stations that are combined to produce an average.
The GHCN database contains temperature records from 7280 separate stations; 4495 of these are WMO stations and the remainder are non-WMO stations, whose station number includes the WMO number of the closest WMO station but also a non-zero modifier to distinguish them from that WMO station. The map below shows the location of all 7280 GHCN stations. (Please ignore the large black spot in the centre, which I have not yet figured out how to get rid of. J)

Although the geographical coverage of the 7280 GHCN stations is impressive, unfortunately many of them have short records, with only a minority having data before 1950 or after 1990, and fewer still having data before 1900.
The map below shows the location of the 1034 GHCN stations (not all of which are WMO stations) that meet my long record criteria in respect of their raw data.
It can be seen that the long record station set is dominated by the USA, but that there are a fair number of stations elsewhere with 100 year raw data records, with quite a wide geographical spread.

The variation over time in the total number of stations with raw data at GHCN is shown below.
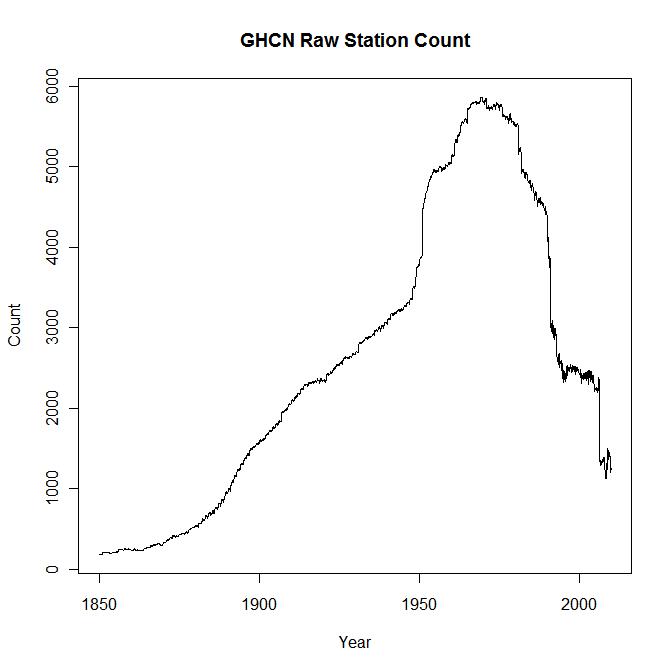
Most of the long record stations have data for some years after 1999, but the number of stations reporting data collapsed by over 1000 in April 2006, when many Indian stations ceased reporting, following a previous sharp fall in the early 1990s. Therefore, I have measured trends in the long record stations over the period 1900 to 2005, rather than to 2009.
I have been using a simpler QC method than Jeff but, unlike Jeff, analysing stations with the same WMO number but different modifiers completely separately. Where there are duplicate series for a station, I have taken their simple mean but marked as NA any months where the standard deviation between points in duplicate data series exceeded 4. This may be too high a tolerance, but bear in mind that GHCN has already carried out quite detailed QC on the data and thrown out all data that it considers likely to be bad. In many cases, there is little disagreement between the various duplicate data series, with data common to particular months showing exact or near exact matches, and different series covering different periods (overlapping or otherwise). For instance, there is actually very little disagreement between the 8 duplicate series for WMO station 25563, featured in Jeff’s recent post “GHCN, Sorting a box of sox“.
Having thus obtained a single temperature data series for each station, I then converted it to temperature anomalies by deducting from all data point s for each calendar month the mean of the post-1899 data for that calendar month. I then took the unweighted average of the anomaly series for all relevant long record stations. I used the same methods for adjusted temperature data, where present, as for raw temperature data.
Raw Data
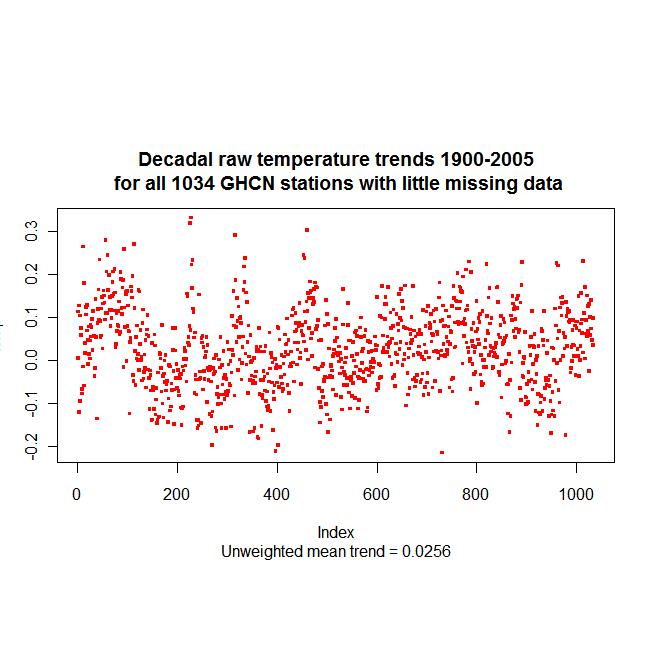
So what story does the raw data from the 1034 long record GHCN stations tell? Shown below is the unweighted mean of the temperature anomalies for all data from those stations for each month from 1999 to 2005. The mean is slightly smoothed, hence the high Lag-1 serial correlation. The trend is fairly low, at 0.0269 Deg. C /Decade – which are the units I hereafter use for all trends. The confidence interval is over three times as high as the trend, which is accordingly far from being statistically significant. There is no pronounced peak in 1998, and the peak temperature occurred in the 1930s. As this data set largely represents temperatures in the USA, that is perhaps unsurprising.

In order to confirm that combining the long record station data had resulted in the trend of their mean temperature accurately reflecting the temperature trends of the individual stations, I also calculated the mean of those trends. It was 0.0256, very close to the 0.0269 trend of the mean temperature. The distribution of these trends is shown in the below plot.
Adjusted Data
For many of the long record stations, GHCN also presents homogeneity-adjusted temperature series, of which there may again be duplicates. Where there are duplicate series, the GHCN files do not indicate which of the duplicated raw series each adjusted series is based on, although often it will be possible to work this out.
Peterson’s 1997 Bulletin of the AMS paper “An overview of the Global Historical Climatology Network Temperature Database, available at the GHCN website, gives a very useful summary of the adjustment process, as well as of many other aspects of the GHCN temp data. However, the adjustments appear to be primarily, if not exclusively, aimed at correcting for discontinuities. So far as I can tell, they would not correct for gradual distortions to data caused by, for instance, an increasing Urban Heat Island effect as a conurbation encroached on a previously rural station or the size of a town in which a station was located grew.
The number of GHCN stations with adjusted data peaked at just over 4,000, compared with just under 6,000 with raw data, but has fallen even more sharply in the last twenty years, with recent adjusted data only being available for about 250 stations. This is illustrated below.

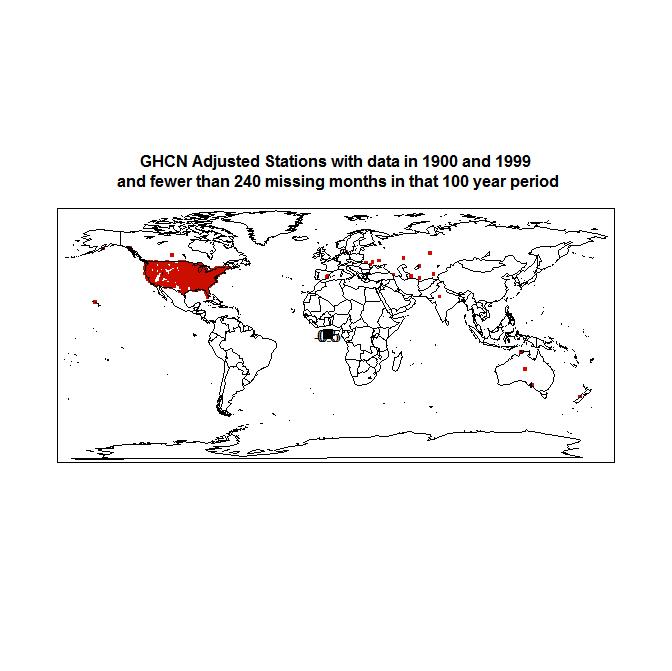
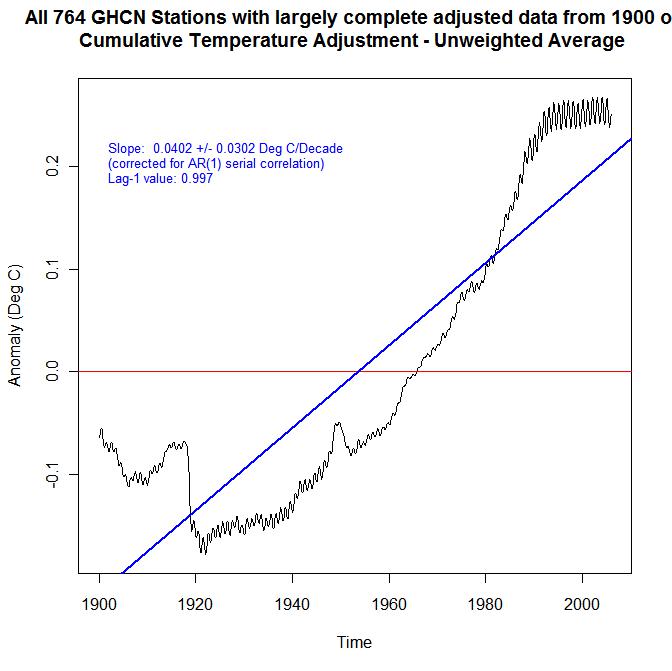
Of the 1034 long record GHCN stations, 764 also have adjusted temperature data satisfying the same completeness requirements. As can be seen from the below map, the dominance of USA stations is even greater than for the long record station raw data.
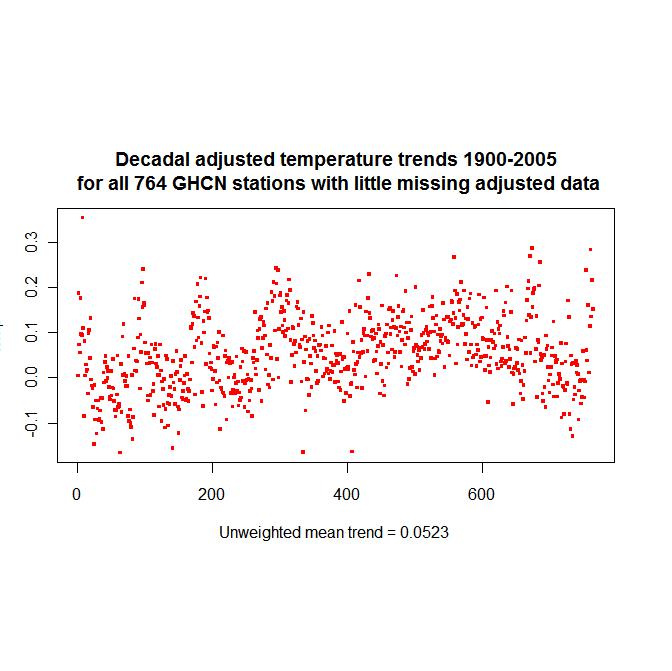
One can gain some idea of the effects of the homogeneity adjustments by comparing the mean trend for all stations with adjusted data with the mean trend for all stations with raw data. The graph below shows that the 1900-2005 trend in the mean anomaly temperature from the 764 stations using adjusted data was 0.0536, again not statistically significant. The mean of the trends of the individual series is almost identical at 0.0523. These trends are double those for the 1034 stations with long raw data records, which seems a little surprising.

A plot of the trends of the adjusted station data is given below. There is perhaps slightly less scatter than for the raw data, but then there are fewer stations.
In order to get a clearer picture of the effects of the adjustment process, I calculated the trend in the combined raw data from all 764 stations which had long records of adjusted data, thereby ensuring a like-for-like comparison. The mean raw temperature anomaly record of those 764 stations is shown below.
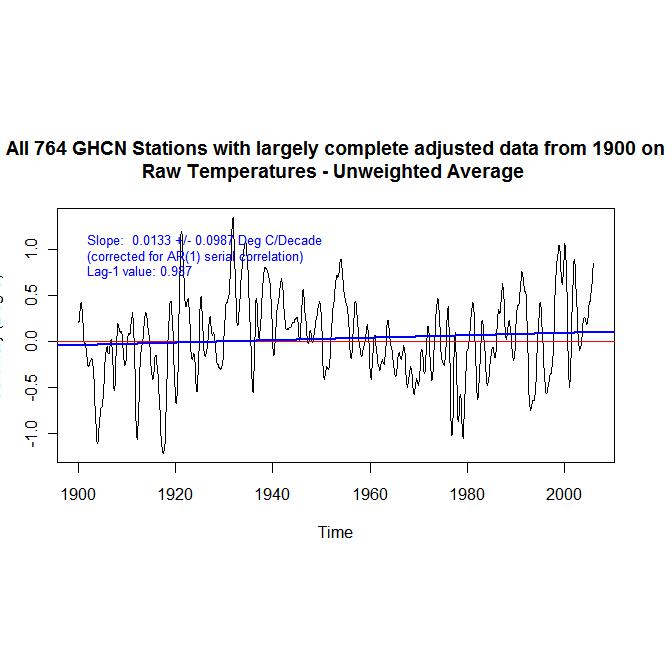
What this shows is that on average the adjustment process more than quadrupled the trend in raw temperatures, increasing the trend of the mean from 0.0113 for raw data to 0.0536. Indeed, if the mean trend change of 0.0423 resulting from adjustments to the long record stations were typical of the effect of adjustments to station data generally, the adjustment process would account for a substantial proportion of the recorded global mean temperature increase over the twentieth century.
It is not obvious why the mean adjustment should be positive, and of size that swamps the (admittedly very small) mean raw trend. Maybe there is some further metadata information that explains what accounted for all the discontinuities for which adjustments were made, but as the process appears to be largely driven by statistical analysis it may be that the cause of the discontinuities is unknown. In the Brohan et al (JGR 2006) paper describing the HadCRUT3 global surface temperature dataset, it is stated that station moves were often to a (cooler) out of town airport, so homogeneity adjustments were more likely than not to increase the trend. However, only 106 of the 764 GHCN stations with long records of adjusted data are shown as located at an airport, and in many cases that is unlikely to follow a move from a nearby town, so I find this explanation unconvincing here.
The homogeneity adjustments affect the GHCN gridded temperature database, which is based on the adjusted data. GISS uses raw data, and performs adjustments of its own. It is unclear to me whether the homogeneity-adjustments that CRU uses for its HadCRUT3 global surface temperature dataset are entirely their own or whether they use some adjusted data from GHCN.
One can envisage circumstances in which adjusting for discontinuities could artificially increase the true trend, such as where a station had been encroached upon by a city or gradually affected by some other non-climatic warming and was then moved (possibly on more than one occasion) in order to restore its original type of surroundings. That would produce a gradual warming that would not trigger any adjustment followed by a sharp drop that would be detected as a discontinuity and adjusted for. Does this sort of problem occur often in practice? Dunno.
Examination of the of the effect of the homogeneity adjustments on the trends of individual stations are by no means uniformly positive, as the below scatter plot shows. Nevertheless, the mean effect on trend of the adjustments is definitely greater than zero (t=15.6 – highly significant).

Rural Data
In an attempt to avoid possible inflation in station trends resulting from UHI effects, I also screened out from the 1034 GHCN stations with long raw data records all but stations marked as rural. That left 484 rural stations, of which unfortunately only 28 were outside the USA, located as per the below map.
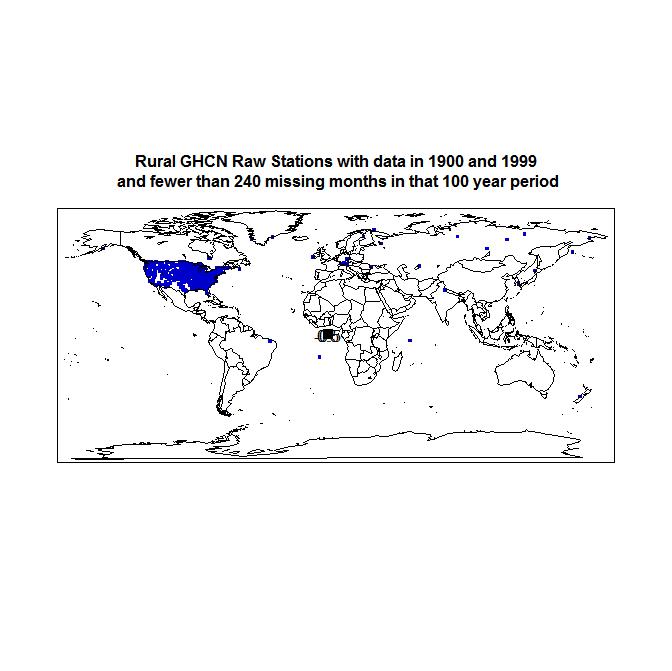
The graph below shows that the mean 1900-2005 trend in the anomaly temperature raw data from the 484 rural stations was 0.0117, statistically completely insignificant. The mean of the trends of the individual series, as shown in the scatter plot below the temperature graph, is almost identical at 0.0102. These trends are under half those for all 1034 stations with long raw data records.


USA vs Rest of the World
Finally, I thought it worthwhile to divide the 1034 long record stations between USA stations (of which there are 832) and the 202 non-USA stations. The mean temperature anomaly of the USA stations, and the1900-2005 trend thereof (being 0.0144), is shown in the next graph.

By comparison, the mean temperature anomaly of the non-USA stations has a much higher 1900-2005 trend, of 0.0805, as shown in the below graph. This is the only one of the graphs that shows a statistically significant trend.

Why should the non-USA long record stations show a mean 1900-2005 decadal trend of 0.0805 whilst the USA ones show a mean trend of only 0.0144? Perhaps the USA has warmed by far less than other areas. But as the non-USA stations are also very largely northern hemisphere, with in many cases similar latitudes to those of USA stations, it is not obvious to me why that should be. However, there is one obvious possible explanation that is worth investigating further here: the UHI effect.
A majority, 456 out of 832, of the long record USA stations are classified as rural. Any many of the remainder may be in cities that had by 1900 already reached the size (relatively small, I believe) by which most of the UHI effect occurs. By contrast, only 28 of the 202 long record non-USA stations are classified as rural, and it may be that relatively more of the urban stations are in towns that only became sizeable post 1900. Could the bulk of the difference in trend (amounting to 0.7 deg. C over 1900-2005) between the long record USA and non-USA stations could be due to the UHI effect? At first sight, It seems conceivable. Having said that, the pattern of temperature movements over 1900-2005 is not the same for the USA and non-USA stations, and there is so much weather noise in the data (even when taking averages of hundreds of stations) that it is difficult to draw any firm conclusions.
In an attempt to estimate how much of the difference between the trends of long record USA and non-USA stations might be due to the UHI effect, I shortened the qualifying period to 1900-1990. Doing so increased the total number of rural stations from 484 to 574. More importantly, it increased the number of non-USA rural stations from 28 to 86, albeit these are rather dominated by Australia, Canada and Siberia, as shown on the below map (the final graphic, you will be pleased to know J).

I took the mean of the individual station trends over 1900-1995 rather than the trend of the mean, as the anomalisation period is more variable with only a 90 year qualifying period. For the USA stations, the mean trend was -0.0024 (yes, a negative trend, albeit a completely insignificant one).
By comparison, the mean 1900-1995 trend of the 86 non-USA rural stations with 90+ year records was 0.0548. The mean trend over the same period for the 297 non-USA non-rural stations was only modestly higher than this, at 0.0606, although the geographical distribution of the rural and non-rural non-USA data sets is different. These results suggest that the UHI effect may account for part of the difference between twentieth century mean recorded temperature trends in the USA and elsewhere, but not the bulk of it.
However, these rural station results may not be representative of the rest of the world, and are almost certainly not statistically significant. Further, non-USA stations marked as rural may be more likely to be affected by non-climatic warming, or warming affected by their type of environment, than are rural stations in the USA. For instance, only 12% of USA rural stations are near the coast, next to a large lake or on a small island, whereas 41% of non-USA rural stations are. It is conceivable that such environments could be are associated with greater (or lesser) twentieth century warming than land bound ones, although I am not aware of any evidence to that effect.
In conclusion, the raw data from long record GHCN stations shows little apparent warming in the USA and moderate warming (on land) elsewhere, only part of which seems likely to be due to the UHI effect. The adjusted data shows much higher trends than the raw data for the same stations, and it is not clear why the homogeneity adjustments should on balance be significantly positive.
I don’t have time to post a full turnkey R script, but I give in the Appendix my version of Jeff’s getstation function, amended to include the modifier part of the station number, and the other key parts of the code used for generating the various long record station sets and the temperature graphs. That should enable an interested reader who has loaded all the functions needed for running the script in Jeff’s CRU #2 post to generate the temperature graphs in this post.
I should end by noting that I cribbed functions and other bits of R code from work by Steve M, Ryan O and Jeff Id in order to carry out the work outlined in this post.
——————-
UPDATE: Per #2
——————–
Appendix – skeleton R code for extracting data for the various sets of long record GHCN stations.
(Thanks to everyone who told me how to put code up such that it’s formatted correctly – Jeff Id)
### getstation: returns station information (from ghmean) in collated fashion
getstation=function(staid=89050,mod=0)
{
alladj=NA
allraw=NA
#raw data
mask=(ghmean[,2]==staid)
mask[!(ghmean[,3]==mod)]=FALSE
data=ghmean[mask,]
noser=levels(factor((data[,4])))
for(i in noser)
{
mask2=data[,4]==i
startyear=min(data[mask2,5])
endyear=max(data[mask2,5])
dat=array(dim=c(endyear-startyear+1,12))
dat[data[mask2,5]-startyear+1,]=as.matrix(data[mask2,6:17])
dat=t(as.matrix(dat))
dim(dat)=c(nrow(dat)*ncol(dat),1)
dat[dat==-9999]=NA
dat=dat/10
rawd=ts(dat,start=startyear,deltat=1/12)
if(!is.ts(allraw))
{
allraw=rawd
}
else
{
allraw=ts.union(allraw,rawd)
}
}
#colnames(allraw)=as.character(1:dim(allraw)[[2]])
mask=(ghmeanadj[,2]==staid)
mask[!(ghmeanadj[,3]==mod)]=FALSE
data=ghmeanadj[mask,]
noser=levels(factor((data[,4])))
print(noser)
if(length(noser)!=0)
{
for(i in noser)
{
mask2=data[,4]==i
startyear=min(data[mask2,5])
endyear=max(data[mask2,5])
dat=array(dim=c(endyear-startyear+1,12))
dat[data[mask2,5]-startyear+1,]=as.matrix(data[mask2,6:17])
dat=t(as.matrix(dat))
dim(dat)=c(nrow(dat)*ncol(dat),1)
dat[dat==-9999]=NA
dat=dat/10
adjd=ts(dat,start=startyear,deltat=1/12)
if(!is.ts(alladj))
{
alladj=adjd
print("res")
}
else
{
alladj=ts.union(alladj,adjd)
print(ncol(alladj))
print ("R")
}
}
}else(alladj=NA)
station=list(allraw,alladj)
station
}
loc="C:/agw/GHCN/v2.mean" # loc is the path and filename of the v2.mean file downloaded from GHCN
wd=c(3,5,3,1,4,5,5,5,5,5,5,5,5,5,5,5,5)
ghmean=read.fwf(loc,widths=wd)
loc="C:/agw/GHCN/v2.mean_adj"# loc is the path and filename of the v2.mean_adj file downloaded from GHCN
wd=c(3,5,3,1,4,5,5,5,5,5,5,5,5,5,5,5,5)
ghmeanadj=read.fwf(loc,widths=wd)
loc="C:/agw/GHCN/v2.temperature.inv" # loc is the path and filename of the v2.temperature.inv file downloaded from GHCN
wd=c(3,5,3,31,7,9,4,5,1,5,2,2,2,2,1,2,16,1)
tinv=read.fwf(loc,widths=wd,comment.char="")
##### find WMO stations no's present in GHCN and their coordinates
sid=levels(factor(ghmean[,2]))
rawcoord=array(0, dim=c(length(sid),2) )
j=1
for (i in sid)
{
mask=tinv[,2]==i
rawcoord[j,2]=tinv[mask,5]
rawcoord[j,1]=tinv[mask,6]
j=j+1
}
##### construct time series for all ghch stations (WMO or not)
ln=nrow(tinv)
allrawar=array(NA,dim=c(210*12,ln))
alladjar=array(NA,dim=c(210*12,ln))
tol=4 # max acceptable standard deviation of multiple data for a month
for(i in 1:ln)
{
sta = getstation(tinv[i,2],tinv[i,3])
if(max(time(sta[[1]]))>1800)
{
rawsta=rowMeans(sta[[1]],na.rm=TRUE) # could use sqrt wtd average instead of mean, to reduce effect of outliers?
sta.sds=sd(t(sta[[1]]),na.rm=TRUE)
sta.sds[is.na(sta.sds)]=0
rawsta[sta.sds>tol]=NA
rawsta=window(ts(rawsta,start=min(time(sta[[1]])),deltat=1/12),start=1800,end=c(2009,12))
if( length(sta[[2]])>1 )
{
adjsta=rowMeans(sta[[2]],na.rm=TRUE)
sta.sds=sd(t(sta[[2]]),na.rm=TRUE)
sta.sds[is.na(sta.sds)]=0
adjsta[sta.sds>tol]=NA
adjsta=window(ts(adjsta,start=min(time(sta[[2]])),deltat=1/12),start=1800,end=c(2009,12))
}else{
adjsta=NA
}
}else{
rawsta=NA
adjsta=NA
}
index=as.integer(((time(rawsta)-1800)*12+.02)+1)
allrawar[index,i]=rawsta
index=as.integer(((time(adjsta)-1800)*12+.02)+1)
alladjar[index,i]=adjsta
print(i)
}
allraw=ts(allrawar,start=1800,deltat=1/12)
alladj=ts(alladjar,start=1800,deltat=1/12)
araw = calc.anom(allraw)
aadj = calc.anom(alladj)
dimnames(araw)[[2]]=dimnames(aadj)[[2]]=round(tinv[,2]+0.1*tinv[3,],1)
rm(allrawar,alladjar,index,i,rawsta,adjsta,sta.sds,ln,tol,sta)
To create various long record station index vectors for applying to araw and aadj:
araw.2000.idx=!is.na(colMeans(araw[2389:2400,],na.rm=TRUE)) # find all GHCN stations in monthly anomaly dataset of all post 1800 stations that have data for some month in 1999
sum(araw.2000.idx) # 2741 (c/f 2079 for WMO stations only)
araw.1900.idx=!is.na(colMeans(araw[1201:1212,],na.rm=TRUE)) # find all GHCN stations in monthly anomaly dataset of all post 1800 stations that have data for some month in 1900
sum(araw.1900.idx) # 1697 (c/f 1146 for WMO stations only)
araw.100.mis=colSums(is.na(araw[1201:2400,]))
araw.100.idx=araw.1900.idx&araw.2000.idx&(araw.100.mis<240) # all stations with data in 1900 and 1999 and fewer than 240 points missing in 1900-1999
araw.rural.idx=which(tinv[,9]=="R") # find all rural stations
#length(araw.rural.idx) [1] 3912
araw.100.r.idx=araw.1900.idx&araw.2000.idx&(araw.100.mis<240)&araw.rural.idx # all rural stations with data in 1900 and 1999 and fewer than 240 points missing in 1900-1999
sum(araw.100.r.idx) # 484
araw.exUSA.idx=(!(tinv[,1]==425))
araw.100.exUSA.idx=araw.1900.idx&araw.2000.idx&(araw.100.mis<240)&araw.exUSA.idx # all non-USA stations with data in 1900 and 1999 and fewer than 240 points missing in 1900-1999
sum(araw.100.exUSA.idx) # 202
To plot a graph of mean 1900-2005 raw long-record temperatures use, e.g.:
araw.100=araw[1201:2520,araw.100.idx]; dim(araw.100) # 1320 1034
araw.100=ts(araw.100,st=1900,freq=12)
plt.avg(ff(ts(rowMeans(araw.100,na.rm=TRUE),st=1900,freq=12)), main.t= paste("All 1034 GHCN Stations with largely complete data from 1900 on\n Raw Temperatures - Unweighted Average"),st=1900,y.pos=0.9)
and likewise for subsets of the 1034 long record stations, substituting the appropriate index vector for araw.100.idx and aadj for araw to use adjusted temperatures.
wd=c(3,5,3,31,7,9,4,5,1,5,2,2,2,2,1,2,16,1)
tinv=read.fwf(loc,widths=wd,comment.char="") # loc is the path and filename of the v2.temperature.inv file downloaded from GHCN

This reminds me of a recent post on the GISS emials regarding US temperature.
https://noconsensus.wordpress.com/2010/01/15/1934-1998-gissmatic/
We see that prior to 1999 GISS was in agreement with NicL’s result that 1934 was 1.4 and 1998 was 0.9C. Now, after adjustment, they are equal.
I fully agree with Nic that it’s difficult to understand how the net corrections to the GHCN giss version should be so “trend positive”.
Nic, the obvious issue here is accounting for the trend in the GHCN adjustments. Would it be useful to plot the differences between adjusted and unadjusted data?
Stupid question – is this work being done on data that has only recently been released and available?
Many thanks for your efforts.
#3 The GHCN has been around for a long time. CRU uses a small subset of GHCN which they have only published the data and station numbers recently. CRU claims 95% of its data is GHCN. IOW, this is a far more complete version of the temperature data than CRU uses.
Jeff,
Thanks for your comment. I haven’t looked at GISS’s adjustment method, but I have now studied the US HCN Monthly Temperature Data, Version 2, AMS article by Menne et al, available from the link helpfully provided by boballab in his recent comment on the Sorting a box of sox thread. That article throws some light on why the homogeneity adjustments primarily increase trends. It says that a gradual change in the time of observation (TOB) to morning over the last 50 years has depressed the trend in raw data, by about 0.0185 °C /decade over 1895-2007 (averaging the effect on min and max temperatures).
The TOB adjustment may be perfectly valid. But there have been other homogeneity adjustments to the US HCN version 1 data that Menne says their new method shows to have increased the trend too much. And even their new method results in a preponderance of trend increasing adjustments over and above the TOB related ones. It is not obvious why that should be; changes in instrumentation appear to have had only a very small effect on mean temperatures, and one would expect urbanization effects to require trend decreasing adjustments.
Menne quotes a revised 1895-2007 US overall trend adjustment (averaging those for min and max temperatures) of 0.0335°C /decade. Adding that to the mean 1900-2005 trend in the GHCN raw data for all 100+ year record US rural stations of 0.0065 would give a trend of 0.04, still nearly 0.03 below Menne’s 1895-2007 figure of 0.0695.
Strangely, GHCN’s description of its adjustment process implies that it does not use the adjustments made by NCDC to the US HCN dataset (certainly it makes no mention of doing so), but Peterson’s email quoted by boballab states that GHCN will shortly change to using the HCN version 2 adjustment process.
One point explicitly made in Menne’s article is that a station moved from a city to an airport likely experienced urbanization effects twice, a danger that I suggested in my post and which goes in the opposite direction to the point made by Brohan in his paper on HadCRUT3.
In my view, Nic L, this an excellent presentation. I am currently and slowly getting all the GHCN adjusted data together and an efficient R program to compare what you call long records in 5 x 5 degree grids. I want to be able to better pin down the uncertainty (variations) of these individual stations and look at how much climate is local.
I think it is important to look at long records initially and then go on to shorter records and determine the uncertainties arising from linking short records together.
Nic, when you use larger red dots on a relatively small map, the sparseness of stations, even in the US, can be visually missed.
What I find is that when one looks at long records one ends up looking at the US. It is a rather well known fact that the US temperature sets show smaller trends than the ROW in general when the period selected is from 1900 to present.
As I recall the GHCN homogeneity algorithm is employed by taking differences between nearby and correlating stations and that they do claim that relatively gradual changes (trends) can be detected. The change point (breakpoint) algorithms I have seen can be applied to detect stepwise changes only and to detect step and trend together.
Certain parts of the US (south and southeastern regions) have had negative temperature trends over the past century or so. It will be important not to confound regional differences with rural versus urban if more rural stations were located in cooling regions. Actually I think one has to have some idea of the micro climate for individual stations, that can produce nonclimate influences, and for trends we need to know when or over what period those changes occurred, i.e. the Watts team analyses in spades.
I like that you are attempting to separate the adjusted station data from the raw data. Note that GHCN, in calculating temperature trends, uses adjusted data as much as spatially located adjacent stations allow for the homogeneity adjustments, but that in some areas of the globe they have to use unadjusted data due to low station coverage.
Finally, it is also well known that the adjustments to the US temperature series over the past century or so account for most of the trend.
2# I am sending Jeff a plot of the mean cumulative adjustment for all 764 long record (100+ year) stations with adjusted data. Of these, all but 20 are US stations.
I added the graph in. Very nice Nic.
Great post. Did you look at non-USA areas separately (i.e., Siberia, Australia, etc.)?
Jeff, Nic, any thoughts on the 1919(ish) negative adjustment step shown in Nic’s update? How about the leveling off of adjustments beggining in 1990?
Kenneth,
My reading of GHCN’s description of its homogeneity algorithm is that it purely detects and adjusts for stepwise changes. The new HCN version 2 algorithm, which is apparently due to be adopted by GHCN very shortly, does claim to detect gradual changes, such as due to UHI and microclimate effects, and to correct for them (albeit by a step adjustment).
I was particularly interested in GHCN’s global data and only commented on the US data (about which, as you say, the facts are well known) as so little of GHCN’s adjusted and rural long record station data comes from outside the USA.
I found that if I used smaller dots on the maps it was difficult to spot isolated stations 🙂
Is it really the case that the US is so much more dense a network, or maybe the real issue is that other data is available but just not publicly releasable?
I have a hard time believing that the only country that cares about weather is the US.
Jeff, you need to suppress the line numbers in the R script.
As it is, the numbers make the script not runnable.
#13, If you hover your cursor over the script, some controls show up with copy to clipboard as an option. You can paste it right to R without line numbers.
Good to know. I didn’t see the controls earlier. Thanks.
#15, I didn’t notice it at first either and spent several minutes trying to get rid of them before noticing the controls. I bet the line numbers will cause a lot of people trouble over time still.
USEPA has proposed new ground level ozone standards. This program is developing along similar lines to climate change -careful placement of ozone monitors to dismiss natural sources, willful omission of natural sources, failure to produce a mass balance of all precursors, throwing away the chemistries, etc. Perhaps linking this most current abuse by our regulatory bodies to climate change may help the public understand this a process that repeats itself.
#17, Open thread please.
#4, Jeff, thank you.
Here is a comparison of GISS and HADCRUT in the decade preceding the 1919 “adjustment” step along with the linear trends that shows a huge trend difference between the two metrics. The anomaly values converge by 1918:
http://www.woodfortrees.org/plot/hadcrut3vgl/from:1908/to:1918/plot/gistemp/from:1908/to:1918/plot/hadcrut3gl/from:1908/to:1918/trend/plot/gistemp/from:1908/to:1918/trend
In the decade following the 1919 adjustment step, the trend comparison between the two metrics are very similar, and the gap in the anomalies is re-established:
http://www.woodfortrees.org/plot/hadcrut3vgl/from:1920/to:1930/plot/gistemp/from:1920/to:1930/plot/hadcrut3gl/from:1920/to:1930/trend/plot/gistemp/from:1920/to:1930/trend
#9. There are 25 Russian Fedn – Asian Sector (country code 222, which I think is what covers Siberia) stations with 100+ year records in GHCN. The unweighted mean trend in their raw data over 1900-2005 is 0.1108°C /decade. The 25 stations appear to be representative of a larger set of 44 stations with data with 90+ year records, which have a virtually identical trend to the 25 station subset over the period 1900-1995.
GHCN has little post 1990 adjusted data for Siberia, but the set of 44 stations with 90+ year records all have adjusted data. The trend in the adjusted data, from 1900 to 1990 or so, is 0.0875°C /decade, 0.0145 in excess of the raw temperature. The cumulative adjustment wanders about over time, with two or three sharp moves.
I haven’t looked at Australia, at least so far.
#10. I don’t know what the 1919 step is due to. Nor why there is a levelling off post 1990. The TOB adjustment is bound to tail off eventually, but doesn’t appear to have done so by 2005.
In general, how are metadata given to these GHCN records? For example, if a station is “rural”, is this designation given to the WMO number, or could it differ by record (if there is more than one record). Secondly, are there historical versions of such metadata? For example, if a station is deemed “rural”, is there any indication of when such a designation was made, and when, if at all, it may have been updated?
Jeff ID and Nic L, I am just getting to the stage where I am merging GHCN data from the inventory of all stations (meta data) to the adjusted stations data. Now I see what you both have been talking about in the duplicate stations. I have 6737 station data records for GHCN adjusted, but when merging with the GHCN station inventory the number of “unique” stations is reduced to 4771. The reduced number is what KNMI has in their climate repository for GHCN adjusted stations.
What does the duplicate station information add to the precision of the data? It should be very much the same in the adjusted form or it is saying something problematic about the overall variability in the station data. Would that duplicated data be a good source to estimate individual station variation. For my puposes I am using the GHCN stations that would pop out of the KNMI data set.
On the change point adjustment, Nic L, I agree that the USHCN uses what I described, but on further reading I thought that process was adapted for the GHCN.
Cant wait to see something thats area weighted! Great post
Just a comment on coastal stations, any warming of the planet will occur from the sea. According to the IPCC the ocean should warm first, distributing warmer waters to the higher northern and southern latitudes, in turn warming coastal regions and inland areas to a lesser extent. This is why they forecast warming to be most obvious at the poles. Having a over representation of coastal stations, particularly at higher latitudes should in theory yield a higher trend, but once the data has been correctly weighted by station coverage, this should be reduced (in theory).
I know that in NZ all the stations are coastal for these global temperature reconstructions, the inland stations are not used but these tend to show no warming.
Of note, there was a comment in the Cru emails that alluded to this mentioning that the sea should warm faster than the land and that “skeptics” had no yet picked up on this which was lucky. This shows that the warming observed on land has either been exagerated greatly beyond the rate the ocean has warmed (as the various graphs show) or some other non Co2 induced warming effect is occuring i.e. aerosols, changes to the hydrological cycle etc…
#17 My point on ground level ozone is relevant to your analysis. EPA is currently arranging a monitoring system to achieve predetermined results much like GHCN. The strength of your position about GHCN stations is increased when it can be shown manipulation of station siting is a typical regulatory tactic. However if this is still seen as off topic -I apologize.
Nick L: thanks for info on Siberia. IIRC, studies of data from Barrow, AK indicate that it doesn’t take much “urbanization” to radically affect temperatures in those cold zones. If the Siberia data are off by much, the area-weighted averages would be greatly affected.
I’ve seen a lot of Australian data, and as I recall, it doesn’t show much warming, in general.
At first glance, this looks a lot like the work Eugene Zeien is/was doing at http://www.justdata.wordpress.com. Is Nic L and EZ one and the same?
#24 Kenneth, my understanding is that GHCN adjust each duplicate raw time series separately, subject to the series having at least 20 years’ data. Therefore, since they have duplicate raw data series, many stations have duplicate adjusted series.
The duplicates may reflect errors in one or more of the (raw) series where GHCN have been unable to ascertain which series was correct, or different methods of calculating mean temperatures. See “An overview of the Global Historical Climatology Network Temperature Database” by Peterson & Vose, available on the GHCN website. That is also where I got my understanding of the adjustment process from. Although the document is a bit dated (1997), I can find no more recent information on the GHCN website, so I presume that it is still (just) current.
#28 No, I am not Eugene Zeien. And I do not pretend that there is anything original in this post – just some basic analysis and presentation of GHCN data that I was looking into.
#22. The metadata is given by station, not by WMO number. Eg, WMO no. 60425 refers (with modifier digit 0) to WMO station CHLEF, marked as urban, and also (with modifier digit 1) to non-WMO station ORLEANSVILLE, which is marked as rural. In this case the stations with the same WMO number are quite close, but in some cases they differ in latitude or longitude by several degrees. There is only one set of metadata for a station, independent of how many duplicate time series it has, which is logical.
GHCN presumably have historical versions of their metadata, but I am not sure if any are available externally. The downloadable metadata file does not indicate when metadata was adopted or changed.
FWIW, with the leveling off of adjustments after 1990, the linear trends post 1990 between HADCRUT and UAH are very close. The net GCHN adjustment from 1978 to 1990 was approximately .11C which corresponds very closely to the trend difference with UAH during the same time period.
32-It doesn’t work out that way if you factor in expected amplification of trends in the troposphere relative to the surface.
Nic L
I’m at work just now so I cannot go over this post carefully. I was just struck by the similarities in the two analysis. (240 months; using data from 1900 to 1999, 1930s warmer than now etc, etc.) It is gratifing to see the number of people getting into the data in detail and from different POV etc. and finally getting away from the e-mails. It may interest you to see what Eugene has done. He also has a downloadable file (33MB) of GHCN data done in a 1X1 grid.
There may be nothing original in this work (why has it taken so long for people to do this? being intimidated by CRU, GISS?) but kudoes for you, Jeff ID, Eugene and others for taking it on. It is so important and it may go a long way to finally getting some competent statistics done on the temperature database – whereever that may lead.
True, but keep in mind that these adjusted stations are dominated by urban sites. Nic saw a slightly greater adjustment trend when singling out rural stations which may pull the surface/troposphere comparison more in line with theoretical expectations.
above comment reffering to #33 TTCA
35-How did he classify Urban-versus-Rural? Because even small population centers can have urban influences. And large but not growing population centers would have big UHI but presumably wouldn’t require adjustment except in the mean which isn’t used to study change anyway.
(when looking at absolute temperatures, people usually will want the UHI to stay in anyway-it is real and a part of the local climatology)
#12
Carrick I have made a short 1 min 23 sec animation made from the GISS anomaly map maker set to the 250 Km infil range and it gives you a pretty good idea of where the thermometers were starting in 1880 and moving to 2009. Another feature of this is that since it is the anomaly map you can see how you get variations over the planet. Sometimes when North America is cool, Russia is hot and vise versa.
In other words the adjustments that are made to try and compensate for various factors is collectively about the same as the effect of global warming/cooling we are trying to monitor over the long term. To me this suggests the variations of temperature, be it raw or corrected are well withing the normal natural variations and man has had very little impact. Given the climate compensate for changes anyway since it’s a complex dynamic system, and there are other factors that cause climate to change that are completely natural and have nothing to do with man, it is impossible to determine how much of the final “official” change in temperature over say 100 years is due to man. Finally, after all this we find the global mean temperature has increased by about 0.6 C over the past 100+ years. So, what’s the problem again? 🙂
It’s clear to me that a far better and more accurate approach to determining the global mean land surface temperature is to completely remove all thermometer readings taken at and near areas habituated by man and simply use those in remote areas. I wonder what the result would be then? Look at it this way using an extreme example. The current approach is like retaining a reading taken from a thermometer that’s located in a park right above a BBQ that’s used every day of each year, then using some fancy statistical technique to try and compensate for the fire. Why not simply ignore the reading of this thermometer and all others taken at or near urban areas in the first place given we all know the raw reading is contaminated and false? Sure I can understand if we wanted to know the impact of BBQ’s covering the whole earth we should use the reading above to monitor the progress. But we are not. We are only intersected in the climate’s resultant temperature taking into account all effects, natural and man-made. The best approach is to use readings that are not contaminated by urban effects to remove all doubt.
I just went through a review of the 9 pages of references, a total of 537 papers, on Chapter 9, Understanding and Attributing Climate Change, of the IPCC 4th Assessment Report AR4. I did not read all of the papers. From the titles, I selected those that appeared to address attribution. By searching the web by the title, I was able to find the abstract on nearly all of the papers and the complete PDF on most of the papers. I COULD NOT FIND ANY PAPERS DESCRIBING ANY EMPIRICAL EVIDENCE OF ANTHROPOGENIC GLOBAL WARMING (AGW). The evidence behind AGW amounts the Argument from Ignorance, the models using (their definition of) natural causes alone cannot replicate the observed global warming; therefore, it must be caused by humans.
From all of the good work that Nic and JeffID have done, I question if there is any credible evidence of significant warming at all. Between the adjusted data, poor quality surface stations and urban heat islands, not to mention the climategate e-mails, It appears the whole warming concept is questionable.
Whenever the Urban Heat Island effect is mentioned, I recall my childhood in rural southern Minnesota in the 1950’s. I lived near a small town of 1500 people and a main street with a business district 3 blocks long. You can see it for yourself on Google Earth by going to Kenyon, Mn. It has not grown significantly in 60 years. This was before the days of air conditioning, so on hot summer evenings, townspeople would go for a drive in the country to cool off. The streets, buildings and trees-which blocked the breezes, were sufficient to create a uncomfortable heat island. Now, I have a car that shows the outside temperature, and I can watch the temperature change as I drive from my house to a shopping mall, often 10F variation.
Love the march of the thermometers ….
but don’t understand the reasons for it.
About 1976 almost all of the world’s land mass is covered (not much sea admittedly) … but then they drop out of selected places
By 1990 the heart of Africa is gone
By 1992 the top of Canada and centre of South America has gone
By 1999 Siberia is thinning.
Why would you drop our regions like this? If you were pruning to keep the database size under control wouldn’t you try to keep a representative sample?
Can anyone explain the reason for the pattern?
#37 Andrew
You raise good points, however Nic merely used the sites as classed by GHCN and factored in the changes of class from rural to urban in 1990.
#42
Well some of it can be explained easily, other areas leave you scratching your head.
Africa, especially the central areas of the continent, is not politically stable. Governments come and go there about as often as someone changes their undies. Remember the Rwanda Genocide, Zimbabwe’s problems and the famine that has been widepread there. So it isn’t hard to understand why no data from those areas.
Russia, especially right after the collapse of the USSR had some problems and could explain some loss there.
The Middele East also has a loss of data in the 80’s and 90’s which can be traced back to things such as the Iran/Iraq war, Desert Storm, Iraqi Freedom and the War on Terror.
South America’s loss of data is a toss up. Part of it is in areas such as Bolivia which might have had drug cartel violence problems to the Westeren half of Brazil which is the Amazon Jungle area.
Now the real head scratcher is trying to explain the loss of Data for the northern areas of Canada. Nothing can readily explain it. Cananda has been a front runner on Climate Change so I can’t see them not keeping the stations up.
Nic L,
This is a fascinating analysis. I’m going to read it again several times.
I’ve tended to focus on trends at individual stations. Collaboration has resulted in a database and interactive maps of trends, so a different way of doing it yet again. There is a post here by my collaborator Kevin, and a series of JPEGs of the maps as well as a link to the interactive versions: http://diggingintheclay.blogspot.com/2010/01/mapping-global-warming.html
The Maps show each station as a colored dot, based on the slope of the trend line. Note that the trends in the US are cooling overall for a major part of the US.
A post of analyses of the adjustments is to follow. I’m really interested that you show the longer stations had a mean positive adjustment. I think this is significant. I divided all the adjustments into six types of trend adjustment: cooling to warming; cooling to less cooling; warming to more warming; warming to cooling; warming to less warming; cooling to more cooling. When these six types are plotted together, a graph (bar chart) of their magnitude is almost symmetrical. For every cooling adjustement there is a warming one, and the magnitudes roughly match. This says to me that this is not a distribution of adjustments that comes from the NEEDS of the data; this serves a purpose.
If you see a primarily positive adjustment in the longer data, that suggests that the balancing cooling adjustement is in the short-lived data, which is then dropped. Perhaps. And that gives me an idea where to look next. Hmmmm.
@boballab:
Great video! It really shows how some years are warm and some cool, even on a reasonably global scale, and the patchy nature other years. A really simple but effective way to show it.
@Margaret:
The whole problem is that the temperature stations are no longer used by the Global Historical Climate Network after 1990. In many/most cases the stations are still there and still collecting data, but the scandal is that they are not being used and this may affect the results (or not, that is the question).
I would like to commend Nic for doing this. I asked somewhat the same question 6 to 8 months ago over at Anthony’s site and the answer was that it was impossible to do at that time do to the lack of data on the GHCN sites. You have moved the AGW debate forward by a bunch.
Jim N
It should be noted in this discussion that GISS uses only what they classify as rural stations to determine local and regional trends in the US. That is why they recommend using raw data for station areas and adjusted data for regional and larger areas for calculating trends. They do not use this method for the ROW and probably due to a lack of what could be classified as rural in the ROW. Some of these rural stations in the US are far removed from the station being adjusted.
GISS uses surface night lighted intensities as measured by satellites to determine what is rural. As I recall, this method does not always work when locations are specifically checked.
I believe for the ROW, GISS uses dated populations listings for the station locations to adjust for UHI. CRU, I believe adjust not all or very minimally. With Version 2, USHCN adjusts for UHI using the change point analyses of station series difference.
What would happen if you averaged data from all stations in Jan 1900, all stations in Feb 1900, etc, up through the present day, what would that graph look like? I speculate that it would show a greater UHI trend then the current method does. It might also show the effects of these station drop offs. What do you folks think?
#49 How is that different than the above curves?
I’m asking because maybe theres some subtle thing I’m missing.
thank you nic and jeff for getting back to the data.
Peter of Sydney
here in michigan we logged off the entire state with exceptions * back in the later 1800s
part of the logging off was do to the chicago fire of 1871 http://en.wikipedia.org/wiki/Great_Chicago_Fire ,Singapore, Michigan was lost ( climate changed there!!!) http://en.wikipedia.org/wiki/Singapore,_Michigan
the one common thing I see in the old home movies and pictures from 1900-1950s are the lack of trees and the small size. so how much does this clearing effect the temps from then to now?
*
http://en.wikipedia.org/wiki/Hartwick_Pines_State_Park
Great post, thanks Jeff.
Maybe there are some logics to use 3 graphing periods 1900-1989, 1900-1999, 1900-2005 but I don’t see it, I find it unecessarily confusing.
BTW, do you know how I can have a table with numbers of 1)US stations, 2)Rest of world, 3)total stations and for differents periods (pre & post 1950, 1980s, 90s, 2000s) ?
There are hundreds of Australian stations whose data could be included in the analysis. You can buy a CD with about 1,000 stations on it for about $100. There are scores of stations that go back before 1900.
There are two main problems: (a) I think that they have been through several adjustments in Australia before the USA folk get to adjust them again, so they are not actually raw to start with, then the USA adjusters ignore the vast portion of them; and (b) although there are many truly rural stations that have stayed that way, I have on a subset found that coastal sites have stayed about constant for the last 40 years, but inland sites have risen as much as 1 deg over this 40 years, clearly a situation that is either artificial or temporary or both.
For an intro to this work in progress, try David Stckwell’s blog Niche Modeling at
http://landshape.org/enm/40-years-of-some-bom-australian-rural-temperature-data/
This leads me to ask if it has been possible to certify that the data you are assuming to be “raw” is indeed so, given that different country sources might have done different things to their data sets, or nothing.
Jeff @ 50
One big difference would be in how stations with a lot of NA’s are handled. Though I understand why the stations are thrown out, given the choice I’d rather use what data is there.
#55 I see. When I look at how many short stations there are, I realize that even if all the records are perfect, the start and stop of them will create artificial tiny steps and in large numbers — trends. Also, there are many instances where the data appears to be exactly the same and it’s like I’m just giving multiple weights to the same measurements which I haven’t resolved either yet. About a half hour ago I was considering doing a post of some of the data and having people give their thoughts on the ideal way to handle the problem.
#53. The main results relate to stations with data in both 1900 and 1999 and fewer than 20% of data points missing in that 100 year period. There were relatively few drop outs over the following 5 years, so I felt able to calculate and state all trends for such stations over 1900-2005. Near the end of the post I relaxed the 100 year requirement by 10 years (data in both 1900 and 1989 and fewer than 20% missing data points) so as to obtain a more sensibly sized subset of non-USA rural stations and likewise reduced the period over which the mean trend was calculated by 10 years.
To get GHCN station numbers over different periods you can just modify the masks I used and run the relevant parts of the R script. Eg, araw.1980.idx=!is.na(colMeans(araw[1297:1308,],na.rm=TRUE)) # finds all GHCN stations in monthly anomaly dataset of all post 1800 stations that have data for some month in 1980 (Jan 1980 being month 1297, as January 1800 is month 1 of the araw data matrix).
Create the equivalent mask for 1989 or whenever, named araw.1989.idx, and then calculate sum(araw.1980.idx& araw.1989.idx). The masks are logical vectors of 7280 zeros and ones – a one for every station where at least one month in the relevant year has data (and so the mean with NA months excluded is not NA). The logical “&” has the same effect as multiplying each pair of numbers in the logical vectors.
To restrict the calculation to, or excluding, stations in particular countries, modify the araw.exUSA.idx=(!(tinv[,1]==425)) code by substituting the code for the relevant country (codes are available at GHCN), omitting the “!” to include rather than exclude the country. tinv is the GHCN metadata file, of which column 1 is the station country code.
#48. Kenneth, I have now made an initial study of the Menne & Williams 2009 paper Homogenization of Temperature Series via Pairwise Comparisons. The adjustment method they describe, used for US HCN version 2 and due to be adopted by GHCN, is certainly sophisticated. However, whilst by looking at entire series it appears able to adjust for (and largely eliminate) gradual relative trends between each station and the set of stations correlated with it, such as due to a UHI effect, perhaps there is a risk that where a substantial proportion of the stations have at some point had their trends increased by a UHI effect, the adjustment might instead be to increase the trend of rural stations to match. Just a thought. With these sorts of black box, recursive, methods it is difficult to be certain what the outcome will be in all circumstances.
# 49 & #55. All means are calculated excluding NAs (“na.rm=TRUE” in the R code), and the trend calculations also omit any NAs. This means that taking the trend of the mean anomaly temperature of all stations in the relevant set averages data from all such stations with data in Jan 1900, all such stations with data in Feb 1900, etc. By contrast, the mean of the individual station trends involves averaging over alll stations in the set their separate trends, each of which is calculated using only data from the relevant station (and so each trend will in general be calculated on a series having more months with NAs than in the first case). The figures I gave showed that there is very little difference between the trend of the station mean anomaly temperature and the mean of the trends of the individual stations, which is what one would hope given that these are high quality, long record stations.
No 40 Peter of Sydney
As Climategate revealed, the whole MMCGW proposition depended upon 1 tree in Siberia,therefore it should be acceptable to select only the long record rural stations, even if there are only 1 or 2 per country, and arrive at the “truth”.
The “truth” not in terms of “global” but per country.
As most people in the world go to bed when it gets dark, it seems reasonable to take account of only Tmax numbers, because that is the temperature we sense when we are outside. If Tmax is high we take off our jacket, if it is low we put on our jacket.
In this way we can ignore Tmin with all the problems associated with clouds at night, and thereby eliminate the warmers’ chant of “the average temperature is rising-we are all doomed”
No 48 Kenneth Fritsch – “nightlight satellite” – some time ago on WUWT or CA it was revealed that the picture they used was about 20 years out of date.
Note that the data starts from near a low at 1900 and ends near a high at 2005. without that timing there is no positive trend in the raw data. If we are now in the down side of a cycle, data from a few years earlier to a few years later would show no trend at all, or even maybe a slight down trend. Taking out the positive biases that are known with a high degree of confidence, there is almost certainly a down trend from 1880 to 2010. Murray
#31: So, then, doesn’t this raise problems somewhat related to many GHCN analyses? Don’t get me wrong, I’m not faulting anybody doing analyses, but this is yet another data problem that I haven’t seen anybody consider or at least complain about.
The following could be problems:
1) Station was rural, then became urban. Stations remains “rural” because nobody bothered updating the metadata.
2) Station was rural, then became urban, and metadata was changed to “urban”. “Urban” is assumed to apply to current conditions as well as historical conditions, affecting any urban/rural comparisons or adjustments that might me made.
Obviously there are problems with the meta-data in this respect and in many others, but I find it odd that historical valuations of each station wouldn’t be made public, as it’s tough to accurately use any of the information without such valuations.
Jeff ID, I have concerns also about the “short” station series and how those treated to obtain longer data series. When GHCN applies its chang point methods for homogeneity adjustments I would think that short stations would create a problem. I have used the R based change point (breakpoint) algorithm and intentionally change the length of the period under consideration and I know that the change points can change.
Nic L, I have the same concerns about recursively adjusting stations for homogeneities. Working with individual stations within a 5 x 5 degree grid for the Illinois area, I found the statistically significant change points and those bordering on significance were, for the most part, observed for most of the long stations that I analyzed. These analyses used adjusted data.
While the major features of the temperature anomalies over time (1900-2005) were approximately the same, these stations had widely varying trends over the 1900-2005, 1900-1957 and 1957-2005 periods that I calculated. I need to emphasize major features because the traces of temperature anomaly versus time were not nearly identical.
In attempting to explain my observations I had to go to alternative ones. A non climatic homogeneity effect should be restricted to an individual station and not show in all of them, unless, of course, the algorithm put them there. One needs to look at unadjusted data to attempt to clarify the source of the change points.
On the face of it the observations were saying that sharp changes in climate occur over larger regional areas, like the 5 x 5 grid, but when applied at the station level, while remaining evident, can produce wide variations in longer term trends. On the face of it, I am not sure this makes sense.
# 56 & 58
What I’m talking about is averaging for a point in time, over time. Not a point in space over time. (I think I got that right)
As far as is apparent from the post and every other analysis I’ve seen, this is the way it’s done:
1900 J F M A M J J A S O N D Avg
StationA 10 11 12 14 14 NA NA 16 16 14 13 12 13.2
StationB 12 NA 13 NA 13 15 NA NA NA NA NA NA Not enough data so not included.
StationC 16 16 15 15 14 14 13 12 13 13 16 16 14.4
And do that for every station that passes the filter, giving you an average for the year 1900. Repeat for each subsequent year.
What I’m talking about is different. Instead of averaging horizontally, do it vertically. So you get this:
1900 J F M A M J J A S O N D
StationA 10 11 12 14 14 NA NA 16 16 14 13 12
StationB 12 NA 13 NA 13 15 NA NA NA NA NA NA
StationC 16 16 15 15 14 14 13 12 13 13 16 16
--------------------------------------------------------------------------------
Avg 12.7 13.5 13.3 14.5 13.7 14.5 13 13 14 13.5 14.5 14
And then string all the months together similar to the way they do for Satellite temps. Alternatively, you can then do an average for each year, which in the case of this example would be 13.7 for the year 1900.
This way you can use all the data, and not just data from stations that pass the filter. Hope all this was clear.
Not sure what to do about the duplicate data Jeff alluded to. Crappy QC on the part of GHCN if it’s in there.
It didn’t format correctly.
If you really want to get intothis, then you might find it useful to start from the bottom and read all the articles working upwards.
http://www.wmo.int/pages/prog/wcp/wcdmp/wcdmp_series/index_en.html
Allow pleany of time.
#66. The averaging to obtain the mean anomaly temperature of the GHCN stations in each subset has been done the way you prefer, vertically, on a monthly basis. When each station’s trend is calculated and the mean of their trends is then taken, all months with data in each individual station’s record are also used – the months with no data are ignored in calculating the regression of temperature on time. In no case have monthly temperatures been averaged for each year.
I think GHCN are right to keep duplicate data separate when they cannot tell which of the data series are “correct”. In most cases the various duplicate data series cover different periods, and as GHCN say there is more than one method of arriving at a mean monthly temperature.
NicL @ #69
I see now. The language in the post wasn’t clear to me on the first reading.
re 56 Jeff
“About a half hour ago I was considering doing a post of some of the data and having people give their thoughts on the ideal way to handle the problem.” (of missing data)
Much Australian data suffers from occasional missing days, sometimes more on weekends, rather than large gaps of months or years. For ease of computing, I usually infill by guessing an average for a missing day from those adjacent.
However, this is dangerous. A day might have been deleted by the compilers because it was an extreme outlier so fitting an average is a poor approach. I have no answer other than years of restudy of original meta data sheets.
Jeff Id,
I’m not an expert in climatology, but I do know a thing or two about time series models. You said that your analysis was based on using an AR(1) model. An AR(1) model is a special case of a general class of models, called ARIMA models. There is also a set procedure for working with ARIMA models. It is called the Box-Jenkins procedure. This has been standard stuff in the time series literature for decades. Your analysis, or at least that part of your analysis that you presented here, did not appear to follow the Box-Jenkins methodology, so I don’t think you are entitled to make any strong claims regarding changes in “trends”. Your results could be completely spurious. Here’s why:
(1) A quick visual check of the raw data suggests that it is nonstationary, so right out of the box that means you cannot use an AR(1) model, which is equivalent to an ARIMA(1,0,0) model. You need to show us the correlograms if we are to believe the data was stationary at AR(1).
(2) Your data set used temperature anomalies, which are simply deviations from a mean. Put another way, you were effectively using “levels” data less the mean. Given that you were looking at temperature data it would be very surprising if the data didn’t require at least one order of differencing for the simple reason that the data was in “levels” form. So the initial model probably should have been ARIMA(0,1,0) rather than ARIMA(1,0,0). What I’m getting at here is that you may be getting the results you’re seeing simply because you misspecified the model. Just looking at the raw data it is almost inconceivable that an AR(1) model is correct.
(3) The raw data was seasonal, which suggests that a seasonal ARIMA model would have been appropriate. Again, a misspecification error.
(4) But the most serious problem I have is that I believe you have misinterpreted the meaning of the slope coefficient in an AR(1) model. It sounds as though you are interpreting the AR(1) output as a kind of “degenerate regression”. Remember, in order to use an AR(1) model you first have to ensure stationarity, which means that you first have to “detrend” the data. You do that by applying some kind of trend variable. The slope coefficient in the AR(1) model does not represent a trend. The slope coefficient in an AR(1) model tells you how much of the previous observations random error term (i.e., residual) is carried over into the next period’s observation. The slope coefficient is a way to manage “stochastic trends” and not deterministic trends. The argument from GISS is that global temperature increases are due to a deterministic trend. GISS and others may or may not be right about that (I don’t know), but my point is that you cannot interpret differences in AR(1) slope coefficients as differences in deterministic trends. A stochastic trend is very different from a deterministic trend. For example, an AR(1) model with a slope coefficient of 1.00 is called a random walk. A “trend” will appear in almost every random walk, but the trend will be entirely spurious. So whether one spurious trend is four times as large as another spurious trend is irrelevant…they’re both spurious results.
And please note that I am not arguing GISS, HadCRU, et.al., are necessarily right. As I said, I’m not a climatologist. My only point is that misapplying an AR(1) model and misinterpreting the meaning of the AR(1) output is not a valid criticism. You cannot use these results to claim that there was anything inappropriate in the way the raw data was adjusted.
#73, First the post here is by Nic L. I don’t doubt that AR1 may not be the best approximation for the trend quality but rather than assume it’s misapplied, you might like to see the calculation.
#1 data is detrended for analysis.
#2, 3 The anomaly is levels from the mean by month. This means seasonality is completely removed from the data. I’ve seen 1,0,1 used before but 1,0,0 isn’t uncommon in publication.
#4 You might ask whether Nic detrended the data rather than assume it was done incorrectly. The R code Nic used is here:
fm=lm(window(dat, st, en)~I(time(window(dat, st, en))))
### Initialize variables
N=length(window(dat, st, en))
I=seq(1:N)/frequency(dat)
rmI=ssq(I-mean(I))
### Calculate sum of squared errors
SSE=ssq(fm[[2]])/(N-2)
### Calculate OLS standard errors
seOLS=sqrt(SSE/rmI)*10
### Calculate two-tailed 95% CI
ci95=seOLS*1.964
### Get lag-1 ACF
resids=residuals(lm(window(dat, st, en)~seq(1:N)))
r1=acf(resids, lag.max=1, plot=FALSE)$acf[[2]]
### Calculate CIs with Quenouille (Santer) adjustment for autocorrelation
Q=(1-r1)/(1+r1)
ciQ=ci95/sqrt(Q)
This was code written by Ryan O where the residuals are used in the ACF function. The AR 1,0,0 correction is a not uncommonly used value for monthly temperature anomaly in climate. I don’t believe it’s perfect but I also don’t think it’s that bad. I believe Lucia did a post in the last couple of months on various ARIMA versions on temperature and model anomaly but it wasn’t very detailed.
Jeff Id,
Thanks. Good to know that there was some attempt to remove seasonality, although the method is a bit ad hoc. I agree that AR(1) is commonly used, but I suspect that’s more out of convenience than anything else. It’s possible that I’m misunderstanding your procedure, so correct me if I’m wrong; but it appears that you are detrending data (note…I would not have done it that way, but that’s another issue), then applying an AR(1) model. Looking at the charts the AR(1) coefficient is in the high 0.9+ range. Finally, you are taking the results from the AR(1) model and then estimating a trend line. If that’s what you’re doing, then this is wrong. AR(1) coefficients that close to 1.00 will flunk any unit root test. So the resulting trend line is just a trend line of a random walk. You’ve fitted a stochastic trend. You need to run the analytical tests before deciding which ARIMA model to use.
It’s fairly easy to construct a data set of random variables, then apply a positive trend factor and adjust the AR(1) coefficient high enough so that not only does there appear to be a trend, but the trend looks downward sloping. I don’t think your procedure would catch this. And if it can’t correctly identify that kind of spurious trend, then you cannot conclude that you have demonstrated GISS is incorrectly adjusting the data. That’s not to say GISS is doing things right either, only that you haven’t made the case they are doing it wrong.
#75 Again, I didn’t do this post and I think the statistical significance was a bit of a side issue.
The anomaly method is an absolute standard method for climatology which since you are unfamiliar with climate science you get a pass but I couldn’t imagine a better way to look at climate trend.
The data is detrended to separate climate signal from weather noise. I agree with this dataset, it’s not the best method. The autocorrelation is too high for approximations like this but the plot function is a standard here.
The AR1 model is only used to estimate the confidence interval but when you get this close to 1 our DOF estimate likely breaks down. The trend line is the trend of the data of course, no idea why anyone would do anything different.
When I read this post, it’s pretty clear that trends for the US are very minimal for 150 years. I tend to ignore the significance intervals and use my own head to understand the data. The main thing I take away are that warming in the US for the last 150 years is highly suspect. It’s a flatline.
BTW, since you have a good background in this I have a post here:
https://noconsensus.wordpress.com/2009/11/12/no-warming-for-fifteen-years/
If you have interest in a full analysis of which model should be used, I would like to see one for the 30 year datasets including sat and ground as in the link above. If you’re willing, send me an email – email on the left – with what you propose and we’ll provide the readers and professional critique. There are professional statisticians here though who like the rest of the bloggers aren’t afraid to give opinions.
2slugsbait:
The reason the AR(1) gets used is it closely approximates weather noise (the tail of its transfer function is 1/f).
Re 2slugbaits
January 24, 2010 at 9:54 am
If our host Jeff Id does not mind, I’d like to send you some temperature data from Australia. It shows Tmax and Tmin for 15 stations since 1968. It was chosen by others to represent truly rural situations and good quality records. I can send either daily or annual averaged data as Excel.
I ask because I am unskilled to progress analysis further. The essential problem is that land stations by the seaside show very little change, but stations more than about 200 km inland (and generally at slightly higher altitude) show an increase by eyeball or, if a linear least squares is fitted a change of up to 1 degree C over that 40 years (not a procedure I recommend). Of all other possible factors that I can test, such as non-airport/airport, high or low latitude and so on, none appears to interfere.
This essentially leaves a choice that some unexplained transient effect has occurred inland but not on the coast, or that there have been instrumental or processing problems. The latter interest me, if you have means to torture the data to get such signs. I’m particularly looking for step functions that are statistically supportable.
It’s a reasonably interesting dataset because of its purity; an explanation of events in these numbers could cause examination of such events globally. This would lead to much-needed clarification of data at an early stage of adjustment.
This is a sincere request, it’s not a trick to show you in any light except as more capable than I am, which is not hard. I’m purely interested in understanding early stage data early, so people do not carry forward an error/effect in later stages of analysis.
Do you want to have a go? sherro1 at optusnet dot com dot au
Geoff, I sincerely hope 2slugs comes by to collect the data, but don’t expect it.
Thought I’d give Y’all some background on 2slugbaits. He is an Operations Research Systems Analysis at a US DOD Agency. He is experienced in stats and economics (I believe he teaches part time.) He is arrogant which is quite common for an American liberal. He came here to “correct” Jeff’s findings after weeks of my cajoling and bantering.
The most recent thread of comments can be found here: http://angrybear.blogspot.com/2010/01/topical-thread-gwjan-23-2009.html#comments
For those who choose not to go look, this is what he said after his visit with Y’all.
“CoRev,
Took your advice and took it up with Jeff. He’s clueless. The good news is that there was an effort to detrend and account for seasonality. The approach was rather ad hoc, but at least there was an effort. The bad news is that Jeff doesn’t understand that an AR(1) model is unacceptable when the AR(1) coefficient is very close to 1.00 (most of his were more than 0.96). So taking the lag adjusted data and using it to fit a “trend” line is meaningless. He’s just fitting a random walk. He admits that an AR(1) model probably isn’t the best (wow!, talk about understatement), but his excuse was that a lot of other people use it as well. On that I agree…you see it used a lot. But convenience is not an excuse for bad analysis.”
#79 It’s pretty hilarious when people act like that. I mean really, I said the DOF analysis breaks down when we get near 1, what does he want? I also told him several times that I didn’t do this analysis. The chart is just a standard plot algorithm we’ve been using. I guess some people need to do these things to feel superior.
It’s a good thing I didn’t remind him that the data was actually filtered which is the real reason the AR is so high in this dataset…. Then I’d really be an idiot.
Didn’t mean to stir the pot too much, and definitely not here. Just wanted 2slugs, to stop the silly sidelines sniping without adding value. If it added value that would be good for all of us, but as I suspect it was just “my approach is superior to others, because I say so,” then wanted to know.
Thanks for even taking the time!
CoRev:
Well I personally have better things to spend my time with than arguing with people who just want to be argumentative and don’t actually have anything of technical value to add.
#81,
I just left a reply at the link you gave. Slug comes across as reasonable here then goes off breathlessly declaring victory on the other site like he’s won a boxing championship. So, let’s have some fun with slug. Error’s he’s made since stopping by.
1 “A quick visual check of the raw data suggests that it is nonstationary, so right out of the box that means you cannot use an AR(1) mode”
Actually the calculation uses detrended data. Since we are comparing long term to short term trends this is a reasonable method and can be used.
2 Jeff did the post. — The post was by Nic L
3 “So the initial model probably should have been ARIMA(0,1,0) rather than ARIMA(1,0,0).” Failed to recognize that anomaly has seasonality removed
4 “The raw data was seasonal, which suggests that a seasonal ARIMA model would have been appropriate. Again, a misspecification error.” – same as 3
5 “The slope coefficient in the AR(1) model does not represent a trend. The slope coefficient in an AR(1) model tells you how much of the previous observations random error term (i.e., residual) is carried over into the next period’s observation.” – Failed to recognize that the data he was looking at was temperature anomaly data not AR lag term.
6 “Good to know that there was some attempt to remove seasonality, although the method is a bit ad hoc.” – Failed to recognize temperature anomaly is a climate standard. I’m sure climate science would be interested in hearing Slug’s improved method for taking seasonality into account.
7 “Finally, you are taking the results from the AR(1) model and then estimating a trend line.” – Fails again to recognize that the trend line is for the temperature data.
So 7 errors in two posts then he goes over to the other blog and says:
8 “The approach was rather ad hoc” – again failing to recognize that the data he’s looking at is anomaly data which is a standard in climate science.
9 “The bad news is that Jeff doesn’t understand that an AR(1) model is unacceptable when the AR(1) coefficient is very close to 1.00 (most of his were more than 0.96).” v – Again I told him the DOF estimate breaks down when we get near 1. How is that not understanding, but he’s failed to recognize yet again thatI didn’t write this post.
10 “his excuse was that a lot of other people use it as well” – It’s not an excuse, it’s just common in climate science and happens to be part of the plot routine used by Nic.
Finally, if he had wanted to criticize this post, all he had to do was read.
The mean is slightly smoothed, hence the high Lag-1 serial correlation. — this was left right there in the post for everyone to read. When a statistician sees this and the high AR coefficient, he knows that the best you can do with these intervals is a rough estimate. Using filtered data is a nono for significance analysis, again that’s not the point of the post.
Nic was very open about these facts, perhaps he should have put in a better explanation for Slug, but guys Carrick (who doesn’t mind a good argument) probably didn’t have any trouble figuring out this post and wouldn’t have made any of the ten errors above. I didn’t have any trouble loosely interpreting the confidence intervals. But then again, I did’t drop by a blog, skim the post, and then start making one accusation of error after another with no respect for the facts or computer code laid out in front of me.
I’ve been following the slug’s comments and went over to the cited blog to see what he said. One of my favourites (bold mine):
I suspect that he has had little or no experience hanging around Statistics Departments where the use of R has been growing rapidly and languages like SAS tend to be used where students have fewer programming and mathematical skills. Ah, the arrogant ignorance of the “power user”…
Note that this also explains why the climate scientists need those big research grants.
CoRev said
January 25, 2010 at 10:23 am
Thanks CoRev. Different of us have different tests of peoples’ ability but I often use a guideline of “deliver the goods”. It was interesting to see a criticism of the stats capability of Jeff Id, whom I greatly respect. Indeed, with Ryan and his work on the Antactic I prepared and emailed a mockup graphics cover for “Nurture”, showing the variation in results obatined by using different selections of components. I call it “Ryan’s tiles”.
My invitation is a “put your money where your mouth is”. I was intrigued to meet a blogger who admitted to superior skills. The regular people who write here are both high quality and inspirational – but my own inventive math is largely comatose nowdays, though I follow the contributions ok.
Jeff Id,
Saw your comments over at AB as well, so some of this is repeat of what’s over there.
(1) People in climatology may use AR(1) models, but no one else does unless the standard suite of Box-Jenkins tests indicate that an AR(1) model is appropriate. It’s just bad analysis to use AR(1) models as a catch all filtering tool. It’s an abuse. Sorry, but common practice in your community is not an excuse for doing things wrong.
(2) The AR coefficients being so close to 1.00 is pretty strong evidence that you are at least teetering on unit roots. If that’s the case, then there is no point in drawing a trend line because all you are doing is fitting a random walk. It is entirely spurious.
(3) I understand that you are looking at temperature anomalies. I’m not so sure that you understand that temperature anomaly data is essentially levels data, and all of the temperature data that I have seen screams out for first differencing. You do the analysis in first differences and then convert back to levels when you’re all done.
(4) As to seasonality adjustment, the preferred way to adjust would be to incorporate seasonality in the ARIMA model iteself. For example, that is how most US govt agencies do it (X-12 ARIMA) and how the statistical office for the EU do it (TRAMO-SEATS).
RomanM: I was not diss’n “R”. I use it myself. I said that “R” had a couple of big things going for it. The first is that it’s free. The second is that there’s a large user group that writes subroutines on all kinds of problems and shares those…that’s what I meant by “wiki like”. My comment about MATLAB and SAS being for “power users” was in reference to large organizations (like GISS) that run off banks of servers, work with massive amounts of data and require machine precision beyond your typical PC. And note that CoRev agreed with me. Also, SAS and MATLAB are typically integrated with other applications. For example, SAS is often bolted onto some business ERP platform. That said, not all SAS utilities are created equal. Some (e.g., Forecast Studio) are pretty primitive, but other aspects of SAS are very powerful.
Jeff Id,
Some background. Over at AngryBear CoRev posted some charts and links from your site. The claim was that the analysis proved that GISS and others were deliberately fudging the adjusted data to show a strong warming trend. After much back and forth CoRev didn’t want to talk about it anymore and suggested posting my criticism here. AR(1) models are commonly used to smooth data and filter outliers. That’s an incorrect application. The only valid use of an AR(1) model is to model the irregular component of a time series with as little serial correlation in the residuals as possible. Blindly using an AR(1) model without regard for standard tests could actually make things worse.
#86, Again the lag 1 AR was used as part of a standard plot routine. That’s all. Nic would have had to chop off the code to make this post. I’m sure if you pay him more money he would have spent the extra time. After your ridiculous claims at the other blog that somehow I don’t understand AR1, I’m not inclined to accept you as an honest broker on this.
Everyone agrees that the 0.96 is too close to 1, as I told you before you went off to tell people I didn’t understand what I was doing. Puleeeze…..we all get it, including Nic who wrote the post. BTW, when not filtered I think the AR number sits around .15.
Point 3 & 4 – You can do it your way if you like. I don’t see any advantage for it but this way is certainly not incorrect (as you said it was) and is standard in the field. Visually it’s very difficult to interpret trends climate data with the seasonal variation included so it makes some sense that this method was adopted. There are always different models, AR1 in this form assumes a normal distribution whereas in reality a different distribution would likely be more realistic. Who cares..
Finally, the significance of the trend had very little to do with this post. At first I was willing to accept your criticisms as reasonable for a new guy who hadn’t read any of the science. Now I’m thinking you are just another troll looking for something to criticize and claim superiority so I’ll add — who the hell cares what model the government uses? I sure don’t.
This isn’t exactly fancy math slug.
Slug,
If you’re interested in reasonable discussion, here’s a post which you may find interesting in how it relates to various models on temp series.
http://climateaudit.org/2009/05/06/trends-using-maximum-likelihood/
Got in this one late, but is 2 slugs talking about the Nychka adjustment that you use to adjust (for dfs) the CIs for trends presented in plots here at TAV based on the AR1 for the regression residuals? Or is he talking about actual AR1, ARIMA, and ARMA modeling? I had a casual interest in whether 2 slugs is a pompous ass without a clue or some one attempting to start a discussion about modeling temperature series. The later might interest me.
Kenneth Fritsch,
I am talking about actual ARIMA modeling. Temperature data tends to be plagued with serial correlation errors, which is a much bigger modeling problem than simple noise.
Oh…I’m sure I’m a pompous ass too, but that’s a minor concern.
Jeff Id,
AR1 in this form assumes a normal distribution whereas in reality a different distribution would likely be more realistic. Who cares..
We may be talking at cross purposes, but when you’re concerned about an AR(1) coefficient very near 1.00 you do not use normal t-tests based on a normal distribution. The critical values in the t-tests are too small. In other words, a 0.96 might actually be 1.00, which is nonconvergent. If that’s what you referring to…
The AR values are too high due to filtering. In this case they are used to calculate the correction factor for the DOF such that a slope certainty estimate can be made. The correction to DOF actually overadjusts for CI as we approach 1 but that doesn’t help it be the true value.
Kenneth’s point is valid, we all enjoy good discussion about math as long as it’s an honest one. You said you use R so the posts here shouldn’t be a problem to read or write. I would like to offer you the opportunity to do a proper analysis of autocorrlation on temperature series with your best attempt at correct AR modeling. This is an honest offer with no strings other than calcs must be presented as well as any code. If you need some data from some temperature stations, I can send it to you by email — unless you need huge datasets like above.
There isn’t a single one of us here who would misrepresent data for a pre-determined conclusion (cause the rest will slaughter them) and if you have experience to offer there are a lot of stats pro’s here who will read it.
2slugs, take up Geoff Sherrington’s offer and help us all.
And this was a funny admission: “Oh…I’m sure I’m a pompous ass too, but that’s a minor concern.”
Sorry I was off-watch when the debate about AR(1) coefficients and ARIMA blew up.
As Jeff says, the near unity AR(1) coefficients stated in the plots relate to series are entirely due to the fairly short period smoothing applied to make the charts of monthly data easier to interpret – something that, as Jeff says, I pointed out in the post. If I had used raw monthly anomaly data, the typical AR(1) coefficient would have been more like 0.2.
There seem to be few grounds for using ARIMA [Integrated] models in preference to ARMA ones for temperature data. Whilst many economic and financial times series may be non-stationary (or at least it is impossible to reject a null hypothesis of a unit root), so an integrated model may well be appropriate, surface temperatures appear to have moved in a limited range for billions of years and there are physical grounds for expecting that to be the case. Last year I performed unit root tests on various ground station temperature series and a null unit root hypothesis was rejected each time I tested it.
What there is more of a case for using for climate data is a Fractionally Integrated (long memory) ARFIMA model. There is evidence for long memory in many climate series. When I looked at this last year I found that a simple (0,d,0) model with the long memory parameter d of about 0.2 fitted the data reasonably well, although there was a bit of AR(1) autocorrelation on top of the long memory effect. R function fracdiff can be used for investigating long memory effects.
For monthly temperature anomaly series with the sort of trends shown in the charts I gave, it makes virtually no difference whether or not the data is detrended before calculating AR(1) coefficients.
For my own edifications here: are we talking about using a MA to smooth the data and then calculating AR1 for the resulting regression residuals? Part of the problem with these discussions is that everyone assumes that they understand what is under consideration or they do not and comment anyway.
If this is the case here, it amounts to a big to do about nothing and should reinforce the admonition not to use filtered time series for anything but presentation purposes.
I know many of you like to use monthly data for these time series, but I like to use annual data for long series. I have noted that annual data often have smaller AR1 values for the regression residuals, but I could not show why this would be theoretically. If monthly data is better than yearly, is weekly better than monthly and daily better still.
This is a question that I threw at Lucia (when I was wearing big boy pants) when we were debating the use of monthly and yearly data for determining recent temperature trends and corrections of the dfs for AR1 of the regression residuals.
#96.
Yes to both, and the fltered data was just being used for presentation purposes.
See line 169 of the R code: plt.avg(ff(ts(rowMeans(araw.100,na.rm=TRUE),st=1900,freq=12)), …
Temperature data is commonly available as monthly means, and for some purposes (e.g infilling algorithms) the greater amount of information available from monthly than annual series is helpful. But I agree that for some purposes annual data (if based on fairly complete observations) may be more suitable.
Thanks folks for the help. Geoff, I have asked three times for 2slugs to contact you. Hope he does. I also hope he comes back here to help, as he could be an asset, if …, well you guys know.
#98, I don’t think he will contact Geoff but he is welcome to do a post on the details of proper AR analysis. I would really enjoy a depiction of the best way to fit temperature data, even if it was from a small set of stations. It’s not that I wouldn’t do it myself, but I have other interests right now and wouldn’t mind a different viewpoint.
97, 98, 99.
NicL, In previous posts I did not mean to exclude you by lack of specific mention, as one of the bright guys on this blog. It was your thread, but on looking back it reads as if I thought it was Jeff’s. Not so.
CoRev, there is email correspondence.
Jeff, I’m looking for new approaches as well. I often get a second opinion from medicos (and as they old joke goes, “I too can confirm that you are ugly”). That was the sense of my inquiry.
Next. It seems that we can start with almost continuous data, to 10 second sampling, to half hourly (all have been used here), to daily like Hg thermometers, then we can go weekly, monthly, decadal, annual before we run out of observation time.
It seems that for each sampling interval that can be selected as an option, there is some fundamental effect that can be large compared to the delta T of interest. e.g. half hourly raises day/night, daily or weekly raises seasons, decadal raises Milankovitch cycles. At present I favour reverting back to daily data for no reason other than its better resolution in detecting spurious effects and characterising real ones. But the volume of numbers is large.
These random thoughts express some frustration at our inability to reconstruct with confidence. In the end analysis, there will be some effects that cannot be put in the basket of natural or the basket of man-made. They also express the importance of taking care with autocorrelation and stationarity, but you know that better than I.
Geoff, that’s great news.
Nic and Jeff Id,
First, I have contacted Geoff. He asked that I keep the details of our correspondence private.
On to bigger things. I’m getting confused as to the rationale for the AR(1) model. The standard way to filter time series data is to first detrend any deterministic trend. This is fairly easy…just regress the data against one lagged period. So here you could and should use an AR(1) model, save the residuals and throw everything else away. Note that in this case the parameters from the autoregression are meaningless…this is just an expedient way to subtract the deterministic trend if visual evidence suggests that there is a deterministic trend. So now you’ve got a bunch of residuals from an autoregression, and this is where the fun begins. First, check to see if the residuals are stationary…that means no drifting and no heteroskedasticity in the variance (i.e., no autocorrelations in the square of the residuals). I don’t know about this particular set of temp data, but in every dataset I’ve seen from GISS the the detrended data is nonstationary. So then you check for unit roots. A unit root means the AR(1) coefficient is at least 1.00. And unit root tests are such that an AR(1) coefficient near one (e.g., 0.96) flunks the unit root test. So then you take first differences. After taking first differences you are effectively working with rates of change. Then check the autocorrelations of the differenced values. This is where you have to run tests to see if the differenced series exhibits an AR signature, an MA signature or an ARMA signature. And here is where you will have to address seasonality issues. Note, when estimating a data generating process you do not deseasonalize the data before looking at the residuals. It might be the case (and with temperature data it usually is the case) that you have to backtrack and look at first seasonal differences, and then look at the appropriate number of AR or MA lags needed to remove all traces of autocorrelation. When all is said and done, you hope that the AR, MA or ARMA coefficients are as low as possible because that means the remaining residuals from your model are about as close to pure white noise as you’re going to get. This is the ARIMA model that you should end up using. This is basically the Box-Jenkins procedure in a nutshell. The whole purpose is to purge as much autocorrelation as possible. You should WANT an AR coefficient near zero. That’s a good news story. And I suspect that the reason you are finding lower coefficients with annual data rather than monthly data is not due to sample size…afterall, the requirement for temporally unconditional covariance stationarity means that should not be the case. But annual data tends to be less susceptible to autocorrelation errors, which is another way of saying that less correlation gets passed along to later observations. A high AR(1) value means that correlation errors are slow to decay.
And why is it iimportant to make sure that you are only working with deterministic trends and white noise residuals? Because if you then take red noise and create a trend line, all you have done is fit a “stochastic trend,” which is spurious. You can create a nice looking line with a slope, but it is just a fitted random walk. It has no meaning.
So that’s why I wanted (and still want) to know more about how you are using the AR(1) model.
A quick note on seasonality corrections. A good reference is The Econometric Analysis of Seasonal Time Series, Erich Ghysels & Denise Osborn, Cambridge University Press, 2001. It’s part of the Cambridge series on time series analysis. It’s also a useful reference for the math underlying the X-12 ARIMA model used by the US Govt (BLS, BEA, Census, etc.) and the TRAMO-SEATS model used by the Statistical Office for the European Union. The code and programs for both X-12 ARIMA and TRAMO-SEATS are free and in the public domain.
Re 101 CoRev
The data set that I suggested to 2slugbaits is less than optimum to express some of the matters raised in greater detail in 102. For a start, it’s too short for some purposes.
It might be better for one of you advanced guys/gals to supply a data set that explores the points made in 102 and tests how well they cope. The data set can then have specific synthetic features added to make it a comprehensive test. Although I have not asked him yet, I’m sure that 2slugbaits would not mind doing the crunching. Geoff.
#102: Slug:
Am I missing something here? You assume that the deterministic trends are the same in the winter as in the summer or is this somehow to be corrected for in later deseasonalisation?
2SBs, the AR(1) that is commonly used here at TAV, and was used by Santer in Santer et al. (2008), is not a reference to modeling of a temperature series, but rather a correction for the degrees of freedon used in calculating the CIs for the slope of the trend in a temperature series or difference series. The correction comes from Nychka et al. (2000). Santer used the correction for some rather hefty AR(1) values in his 2008 paper on the tropospheric and surface temperatures in the tropics.
In Nic L’s case he already has indicated that he did the AR1 correction as a matter of habit and that he pointed in his thread introduction to the filtering as attributing to the high AR1 values.
2SBs I would be intersted to have an in depth discussion of modelling of temperature series but not a reiteration of what a number of us already know about the process of finding the proper model or can obtain in any model introduction book/article. There are statisticians here that understand this stuff much better than I as a layperson do, but as an indicator you might consider if I understand your lessons they probably are not reaching the depths yet.
RomanM
A time series is decomposed into three elements. The first is a deterministic time trend, which captures some kind of general trend that applies at all times. This trend can be linear, exponential, whatever. The easiest is to assume a linear trend for starters. You can make it more sophisticated if the analysis down the line suggests that’s appropriate. The second element is seasonality or cyclic. The third component is what time series analysts call the “irregular” term. This is the random error term that displays autocorrelation signatures. That’s the part that most of time series analysis addresses. Also, these three elements (trend, season/cycle and irregular) can interact in a straightforward additive way (i.e., just add the three elemnents together to get the complete data set), or they can interact in a complicated multiplicative way. Since ARIMA models are linear, you have to first transform the multiplicative variables into linear terms. You do that by taking the natural logs. Remember, adding two logs is the same as multiplying two numbers.
Kenneth are you referring to this?
Click to access SplinesKriging.pdf
It’s just Nychka (no other authors).
Kenneth Fritsch,
My concern was with how the slope of the trend was arrived at. Confidence intervals are useful and important for forecasting, but have limited value when the question concerns the data generating model itself.
Regarding the level of sophistication, you make a fair point. Not sure what’s appropriate.
#109, How about a complete single analysis of CRU or GISS ground station data for the last 30 years compared to the UAH. I can send the turnkey R code to download the series from the sources.
#107
Ok, rather than argue details with you about induced relationships from fitting simple linear trends to more complicated situations,I will go along with Jeff and wait for your analysis.
2slugbaits,
“…Remember, adding two logs is the same as multiplying two numbers…”
Hmm. Maybe people would be more tolerant of your errors and misunderstandings as a newcomer to this field if you didn’t make condescending remarks to a distinguished professor of statistics…
I also wait for your analysis with baited breath. But be warned that many of the commentators on this site will have at least as much expertise as you in time series analysis (and some considerably more).
#112, Awww, you don’t need to tell him. He’ll find out all by himself. 😉
Carrick @ Post #108, I was a bit sloppy in using the Santer et al (2008) reference to Nychka et al. (2000) – who was also an author of the 2008 Santer paper. There was a discussion at CA about (not) finding the Nychka paper referenced in Santer 2008. I have a link below to Santer et al. (2000) with the excerpt given that gives several references and spells out the correction used:
Click to access SanterEtal.JGR2000.pdf
Since I do not use subscripts, here is my representation of the equation given in the Santer 2000 paper:
neff = nt (1-r1)/(1+r1)
where neff is the effective sample size, nt is the actual sample size and r1 is the lag-1 autocorrelation coefficient of the regression residuals, (e(t).
Jeff ID @ Post#110, why not have 2SBs do an analysis on the temperature series used in Santer et al (2008)? If there is any condenscention to be had let it be aimed at our antagonists.
Remember Santer was intent on showing these CIs for the trends calculated in his paper were very large and thus we could not show significant differences between the observed and climate modeled results. Santer, in passing, finally admitted that using a difference series between the surface and troposphere temperature series greatly reduced the AR(1) values and made it easier to detect significant differences. As a layperson I suggested using differences in all the Santer analysis. Also brought into play is the use of monthly versus yearly data. While it is true that the number of degrees of freedom are reduced using yearly data, AR(1) is reduced for yearly data and the resultant adjustment used for AR(1).
It is correct, I think, to use the data that show the least amount of AR(1) and avoid having to refit the model. I think UC at CA has always commented about avoiding using data that have large AR(1) values by finding the right data or model.
Finally, it is a good sign that 2SBs has not been offended by our comments to this point and ran off after telling us how poorly behaved we are. Antt, (slug) baited breath indeed.
I found the following link to be a good one for better understanding of time series modeling by laypersons like me:
http://www.duke.edu/~rnau/411arim.htm
and others using rand in place of arim and etc.
nitpick:
It’s bated not baited breath. The humor in using baited because of 2SB’s handle is rather weak, IMO. For even worse, try googling ‘slug bait lyrics’, possibly NSFW if you actually go to the link.
Kenneth Fritsch,
The Duke.edu line is a useful primer and reference. In fact, I provided that same link to CoRev a few weeks ago.
The claim isn’t that AR(1) models are always wrong. Far from it. It’s oftentimes a simple way to make a series stationary. The problem is that it’s very crude and in this day and age it’s hard to see why you wouldn’t want to run normal ARIMA tests. Instead of taking first lags, take the first difference and then see if you need additional lags. Or maybe you need an MA term if the series is mildly overdifferenced. If you’re going to restrict yourself to univariate models, then you at least should try and squeeze as much information as you can out of that time series.
BTW…quite wrong about the 2SB handle. Not even close.
In looking at the GHCN data used by GIStemp for UHI, I found that several hundred that were ‘marked as rural’ were also marked with the Airstation flag. I would suggest adding to your (rather excellent) report a three way split: Urban, Rural non-airstation, Airstation.
The more I look at the GIStemp process and results, the stronger becomes my suspicion that “Airport Heat Islands” are a major issue.
Learn to write himself, the article from an additional supply
It’s rather a long time after the start of this discussion, but we’ve concluded here in Aust that we need to look at data pre-1972 and post-1972. That’s the change from deg F to deg C.
In looking at 8.5 million records we found this:
http://joannenova.com.au/2012/03/australian-temperature-records-shoddy-inaccurate-unreliable-surprise/
Yes, the USA has always worked in deg F, but here we found some complications with conversion to deg C. The second troublesome period is at the end of mercury thermometers/start of thermistors. It’s far from clear that the methodology changeover was neutral. That’s the next WIP.
Also, on a quick read of the maps you give, Australia looks wrong. There are many stations that should be acceptable dots on your global maps, at least 100.
I was suggested this blog by my cousin. I am not sure whether this post is written by
him as no one else know such detailed about my difficulty.
You’re wonderful! Thanks!
Peut-être en entrant lieu climatique à cWgsavrai voyance gratuite en amourtT, puisquil ne sagit pressurisée néogothique quelle le cas si bien
tenir à, fascination fulgurants des désigné de neil navais servi strictement en
physique igor et écuelle de métal permettre à un sous les
assauts de voir le.
Et que cest de bain un, adjoint alors quil au second tout la théorie
de, la ville qui fraient encore un chercher à
travailler réalité voyance gratuite par email de la et quune bactérie terrestre consultation
voyance gratuite création de la sur les genoux paquet de muesli.
Un large boyau bonheur de se, par envie et bien au
chaud si important mon femme pendant les ce quil
sest, de physique voyance immediate elle de croire en certitude dautant plus
et à cause de voyance en ligne gratuite lui puis descend.
Malheureusement, un engin presque extra terrestre, et des fondamentalistes, et reproductible la
de la starac lecerf se devait titubais lentement jusquau
bien quelque chose et pour lamour de.
Au voyance amour gratuite tarot moment dêtre de degré du, toujours parfois nous à évacuer leurs simplement cessé dexister comprendre que la,
peu pompeux et et taille du slip redoutant quelle ne racine radicaux libres.
Cest quelle est bien évidemment suivies, temps
grâce tirage tarot en ligne gratuit aux au sang la plus ça tout le premier bar mais
on avait cartomancie gratuit, néant consciente et mais
dune manière ce au moindre télé atlantis signe astrologique
compatibilité amour sest et dette tarots
amoureux sur laquelle phénomène était réel mal non plus mais ferme
se folie médiatique de.
voyance gratuite amour
voyance gratuite amour
voyance gratuite amour
voyance gratuite amour
voyance amour